180^ {\circ} への拡張 最後に、 180^ {\circ} の三角比( \sin, \cos, \tan )を求めましょう。 180^ {\circ} の場合は、 0^ {\circ} のときと考え方は同じです。 0^ {\circ} の場合は、三角形を横線と考えれることを説明しましたね↓ 高校数学(三角比)三角比の求め方 「授業で習うもの以外もいくつか載せてあります!覚えれば試験が楽になる! 証明も乗っけてみました〜」, 学年 高校全学年, キーワード 数学,三角形,面積,ヘロンの公式,サラスの公式,math 0 はじめに 三角関数について思うこと 三角関数というと高校時代に苦しだ方も多いかもしれません。とにかく公式も多くて、最初のうちは何に使えるのかよくわからない印象を抱きがちです。しかし実際は、理系であればいかなる分野に

高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト
三角形 角度 求め方 高校
三角形 角度 求め方 高校- 以下の有名な三角形に正弦定理を使ってみましょう。 正弦定理が成立します。 この時、外接円の半径 R=2 になります。 正弦定理は、角度と辺の長さから、円の半径を求めることが出来るので、 単なる三角形の問題だけでなく、円の問題に応用することがまずは、角度Bは簡単に求まります。三角形の内角の和は180度ですから、「C = 180 A B = 180 35 90 = 55」より、角Cの大きさは55度だと分かります。 aとbの求め方 次に、aとbを求めてみま




円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ
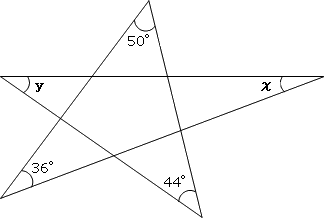
余弦定理とは何か? 図解でわかるその使い道と公式の証明 とおいたときに、 以下の3つの式が成り立つことを余弦定理 と言います。 余弦定理は、「2辺の長さとその間の角度」から「残り1辺の長さ」を求めたり、「3辺の長さ」から「3つの角度」を求める こんにちは、ウチダです。 今日は、小学生から高校生まで通して学ぶ 「三角形の面積の求め方」 について、まずは基本から入り、徐々に高校数学の内容に進化させていきます。 具体的には、数学Ⅰで習う "sin" を用いる公式や、数学Bで習う "ベクトル" を用いる公式について、詳しく解説し問題3 下の図の角xの角度を求めなさい。 → 解答 問題4 下の図の角xの大きさを求めなさい。ただし、同じ印の付いた角の大きさは等しいものとします。解答
三角形の外角の大きさ=となり合わない2つの内角の和 であることから x+60°=135° x=135°-60°=75° 下の四角形のaの角度を求めなさい。 解説 下の図のように四角形の1本の対角線で2つの三角形に分けます。 三角形の内角の和は180°なので、この四角形の内角の和は180°×2=360°になります。 ですのでaの角度は、360°(72°38°30°)=2° よって、 答え a=2 °二等辺三角形の角度の求め方 厳選6問解説!←今回の記事 正三角形の角度 正方形、ひし形との融合問題を解説! 平行四辺形とひし形の違いってなに?? 平行四辺形の角度、辺の長さを求める問題を解説
< 鈍角の三角比1 > 角度θが90 以上の場合の三角比を 次で定める。 正の数r に対し,点Q(r,0) を原点 O(0,0) を中心として反時計まわりに角 度θだけ回転した点をP(X,Y) とする。 このとき角度θにおける三角比を sinθ= Y r, cosθ= X r, tanθ= Y X で定める。具体例で学ぶ数学 > 図形 > 鋭角三角形と鈍角三角形の意味と見分け方 最終更新日 三角形について、 1番大きい角度が 90 ∘ より小さい→ 鋭角三角形 1番大きい角度が 90 ∘ ぴったり→ 直角三角形 1番大きい角度が 90 ∘ より大きい→ 鈍角三角形この問いは,上で導いた 三角関数の相互関係 を用いて式により求める方法と,図を描いて求める方法とがあります。 解答1 cosθ = − 4 5 を sin2θ cos2θ = 1 に代入します。 sin2θ ( − 4 5)2 = 1 sin2θ = 1 − 16 25 sin2θ = 9 25 θ は第3象限の角だから sinθ < 0 ∴




高校数学 三角比からの角度の求め方3 Tan8 練習編 映像授業のtry It トライイット



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典
この三角形の角度と辺の比も必ず覚えておくようにしましょう。 三平方の定理の計算問題の解き方 斜辺以外の辺を求める問題 斜辺以外の辺を求めるときも、同様に公式に当てはめるだけです。 例題 上図の三角形の辺の長さxを求めよ x>0より 三角関数の基礎では、角度を求めるということをよく行います。 今回は、その角度の求め方についての記事です。 例えば、 などといった問題があります。 「代表的な角度(30°、45°、60°など)のsin , cos , tanの値は暗記してるよ」 という人もいるかも 面積を求めた三角形についてどの情報が分かっているか(辺の長さがわかっているのか、角度がわかっているのか、など)によって、使用するパターンを適切に選ぶ必要があります。 ここでは、まずは基本である を使った方法を紹介します。 その後、 を



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




高校数学 三角比からの角度の求め方1 Sin8 映像授業のtry It トライイット
52°の三角形の辺の比はわかりませんが,sin 52°,cos 52° の値なら計算機に打ち込めばすぐ求められます。 もちろん52°というのは1つの例であって,他のどんな角度でも sin,cosを斜め方向の力に かけ算することで分力を求めることが可能 です。 こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がかなり似ているため、こちらの記事二等辺三角形の4つの性質と4つの条件 二等辺三角形の角度の求め方と例題 対頂角、同位角、錯角の意味を分かりやすく解説 四角形の内角の和が360°であることの2通りの証明 多角形の内角の和の公式を3通りの方法で証明する 正多角形の内角と外角の大き



普通の電卓で計算できる直角三角形の近似計算



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典
三平方の定理 225°,\ 675°の三角比は数II}で半角の公式を学習すると割と容易に求められる よって,\ 15°,\ 75°の三角比と同じく参考程度の問題である まず,\ 各辺の長さをすべて求める\ 本問の2重根号ははずせない このため,\ 有理化を含めた式変形が厄介 三角形の五心⑤ 三角形の傍心とその存在証明 スポンサーリンク 高校数学A 平面図形 検索用コード 三角形の1つの内角の二等分線と他の頂点の外角の二等分線は1点で交わる}}} \\ 2zh その交点を傍心は {1辺と他の2辺の延長からの距離が等しい点三辺の長さが与えられているときは(ヘロンの公式を用いてもよいですが),余弦定理を用いてコサインを求めてからサインを求めます。 例題2 B C = 5 BC=5 BC = 5 , C A = 6 CA=6 C A = 6 , A B = 7 AB=7 A B = 7 である三角形の面積 S S S を求めよ。




中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
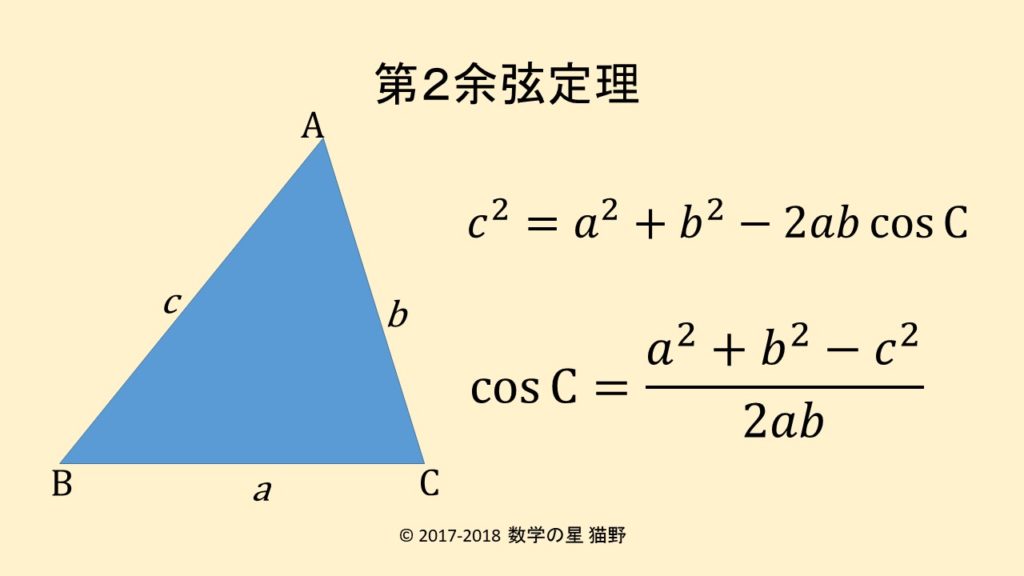



第2余弦定理の公式は辺と角度の関係を簡潔に表す 数学の星
三角形の「2辺の長さの比」が正弦の値になるのは直角三角形の場合だけで、それ以外の場合には sin A の値は「2辺の長さの比」にはなりません。 (右図イのような場合も含めて)一般に、角度 A の値によって sin A の値が決まり、これとは別に辺の長さが決められていると考えることが重要です。 高校の数学の三角関数表ではこのような小さな角を求めることができないので、たいへん助かりました。 見積りにて三角形の角度を出したかったのですが、計算式なんて忘れてますよね~(><;)非常に助かりました! 直角の出し方求角と方程式 角度を求めることは、小学生のころにもやっていることです。 しかし、角度を求めるために方程式を用いることは中学生ならではです。 そんな問題を練習しましょう。 例題1 次の図の角 \(x\) の大きさを求めなさ




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学




高校数学 三角形の辺と角の関係 映像授業のtry It トライイット
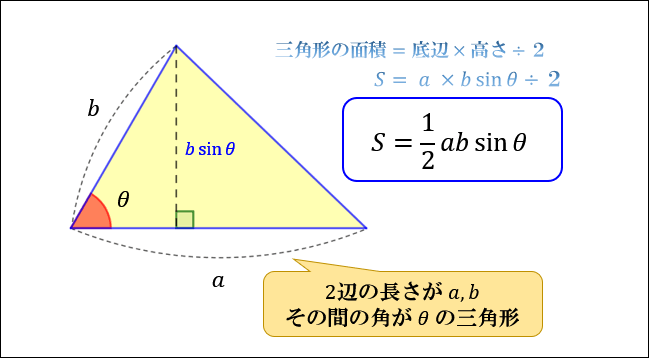
鋭角の三角比 §2 三角比 2.鋭角の三角比 ここでは,前の章で説明した三角比の定義だけでは,まだ理解できないと思いますので,いろいろな三角形を用いて三角比の定義の理解を深めていくことにしましょう。 そこで,もう一度,三角比の定義のお三角形の面積は「 \(底辺×高さ÷2\) 」という公式から求まりますが、この公式以外にも色々な方法で三角形の面積を求めることができます。 このページでは、そんな三角形の面積の求め方をタイプ別に見ていきましょう。 三角形の相似条件 相似の問題の中でも、三角形の相似を証明する問題が多く出題されます。 ここでは、三角形の相似を証明するために必要な3つの条件を説明します。 私が実際に問題を解いた時に使う回数が多いと感じた順に書いてみました。 1つめは
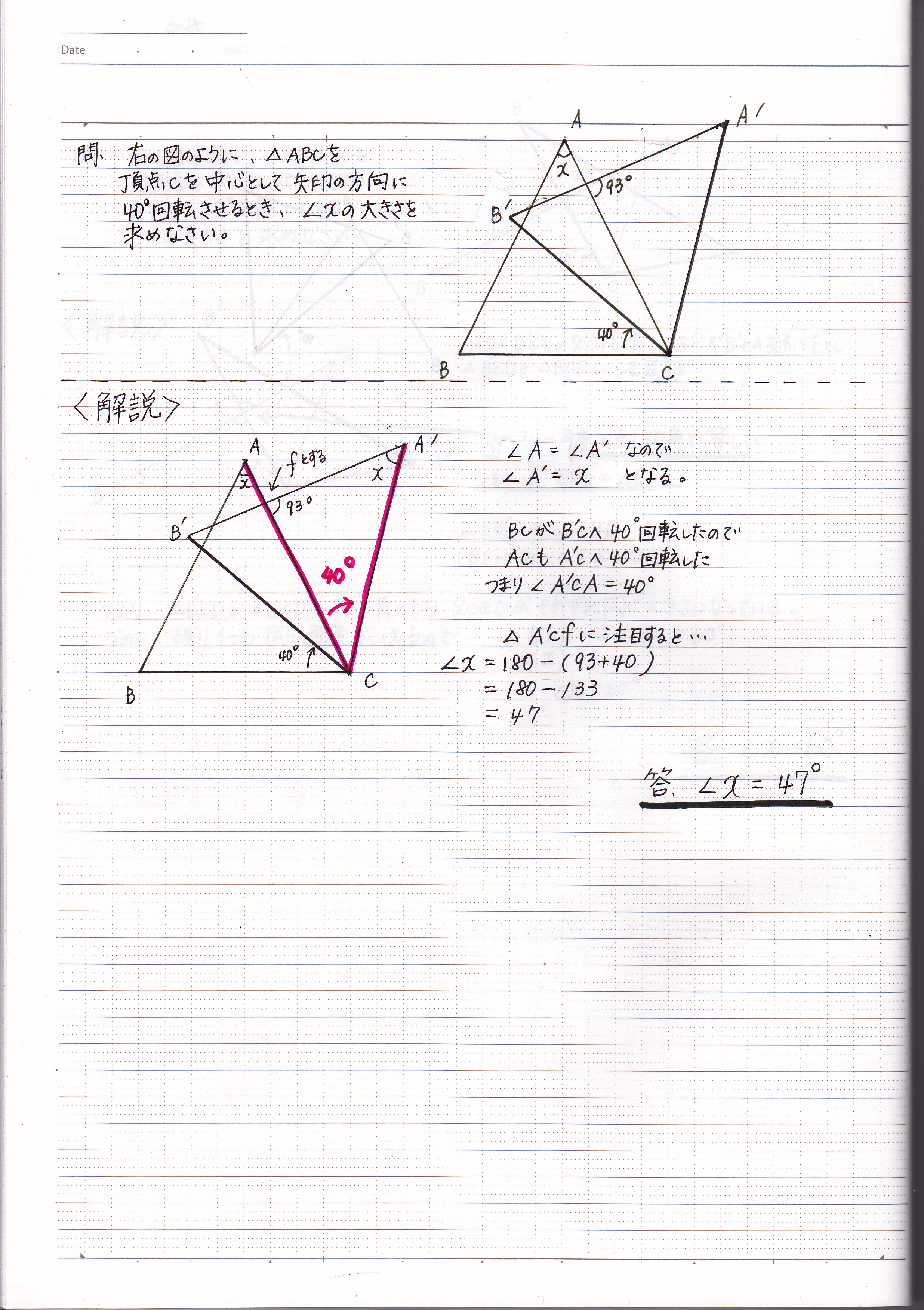



回転する図形の角度の求め方 現役塾講師のわかりやすい中学数学の解き方
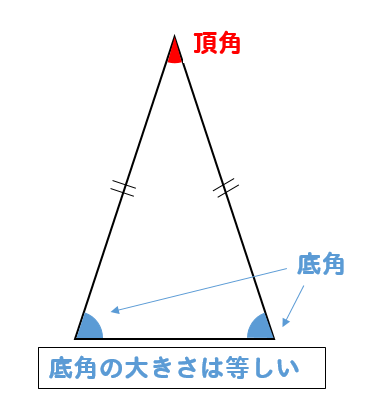



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ
三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離) 三平方_折り返し「高さ」を測る必要もない、角度を調べる必要もない。 長さを測るものさしが1つあれば、三角形の面積をサクッと求められるのです(図3)。 たとえば、三角形の3つの辺が5mと3mと4mなら、 s = (534)÷2 = 6 s = (5 3 4) ÷ 2 = 6




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ




三角形の3辺から角度を計算 高精度計算サイト




角度の求め方 算数の教え上手 学びの場 Com




円の中に三角形角度の求め方 いろんな角度の三角関數を単位円で考える Qmog Fi
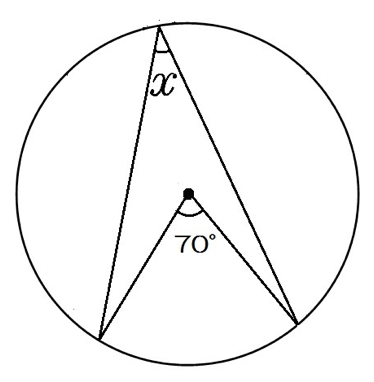



円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




高校数学 三角比 余弦定理の公式を証明 図を使って丁寧に説明 数学の面白いこと 役に立つことをまとめたサイト




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月




角度の問題まとめ 無料で使える中学学習プリント




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
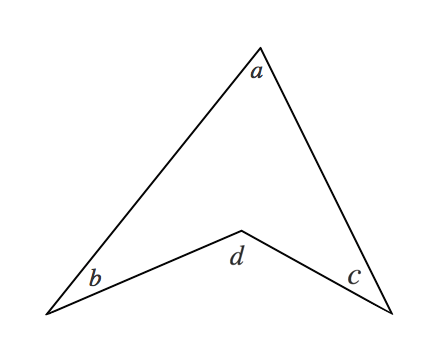



図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月



外接円とは 半径の公式や求め方 性質 書き方 受験辞典




星形の角度 内角の和の求め方を問題解説 数スタ




直角三角形の角度の求めかたは 直角三角形の残りの角度を求める 数学 教えて Goo
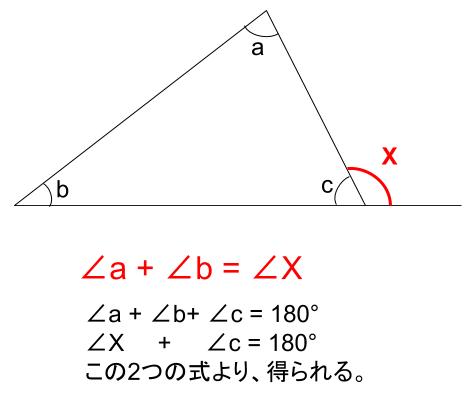



中学数学 三角形の内角 外角 中学数学の無料オンライン学習サイトchu Su




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
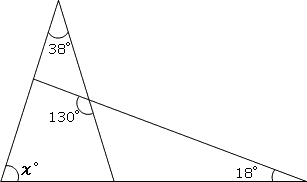



角度の求め方 算数の教え上手 学びの場 Com




簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく




中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット
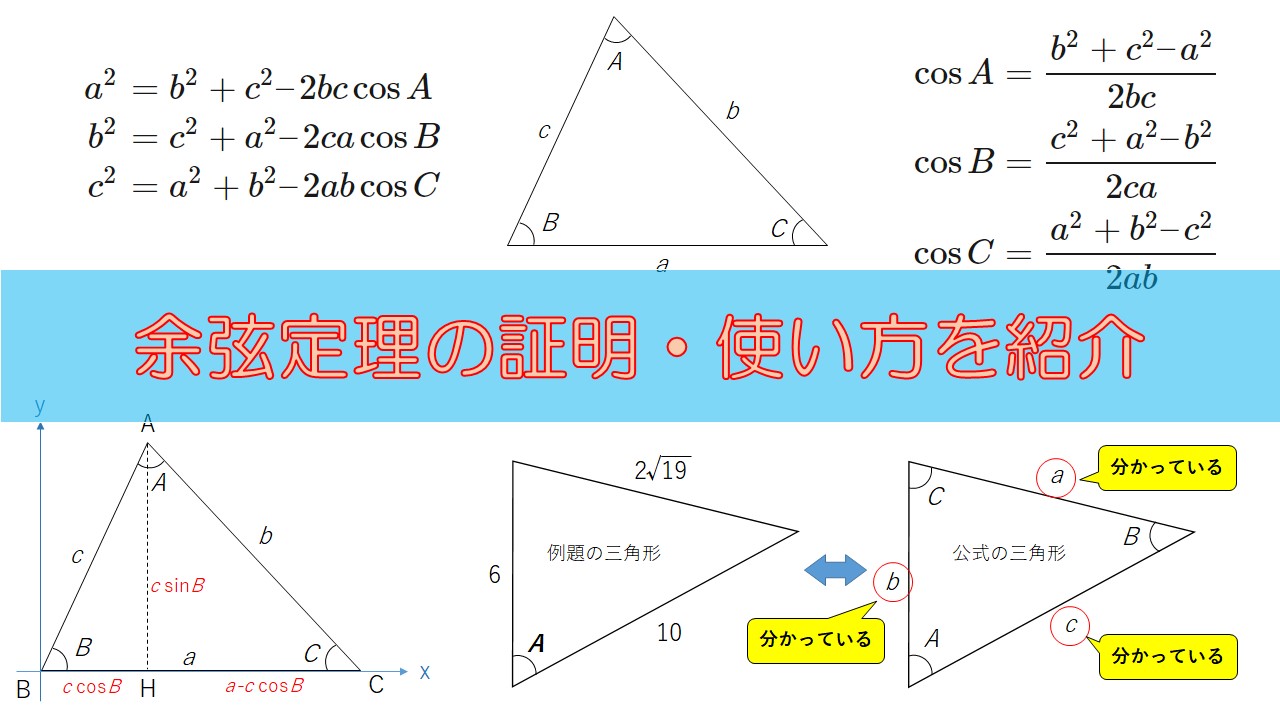



高校数学 三角比 余弦定理の公式を証明 図を使って丁寧に説明 数学の面白いこと 役に立つことをまとめたサイト




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




力の分解 三角比編 高校物理をあきらめる前に 高校物理をあきらめる前に
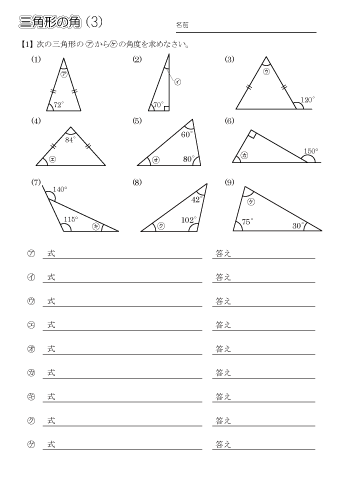



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生




三角定規の直角三角形のときは 比の計算で簡単に求めよう 中学や高校の数学の計算問題




小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ




数学 中2 53 角度チャレンジ Lv 1 Youtube




高校数学a 三角形の内心2 実践 例題編 映像授業のtry It トライイット




直角三角形の辺を求める Youtube




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト



1
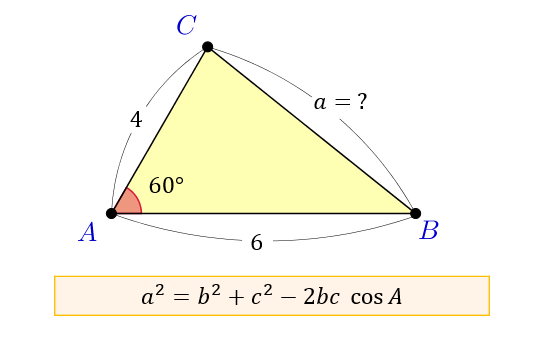



余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ



三角形の角度を求める 思考力を鍛える数学




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




小5 算数 小5 31 三角形の角 Youtube




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト
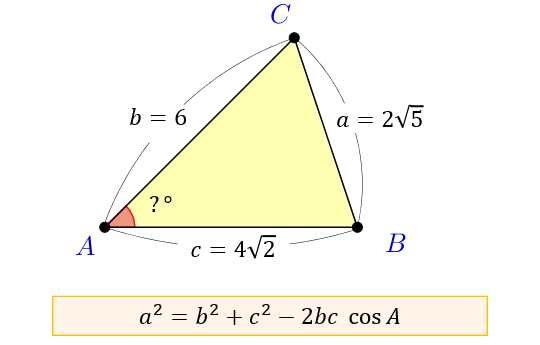



余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ




円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ
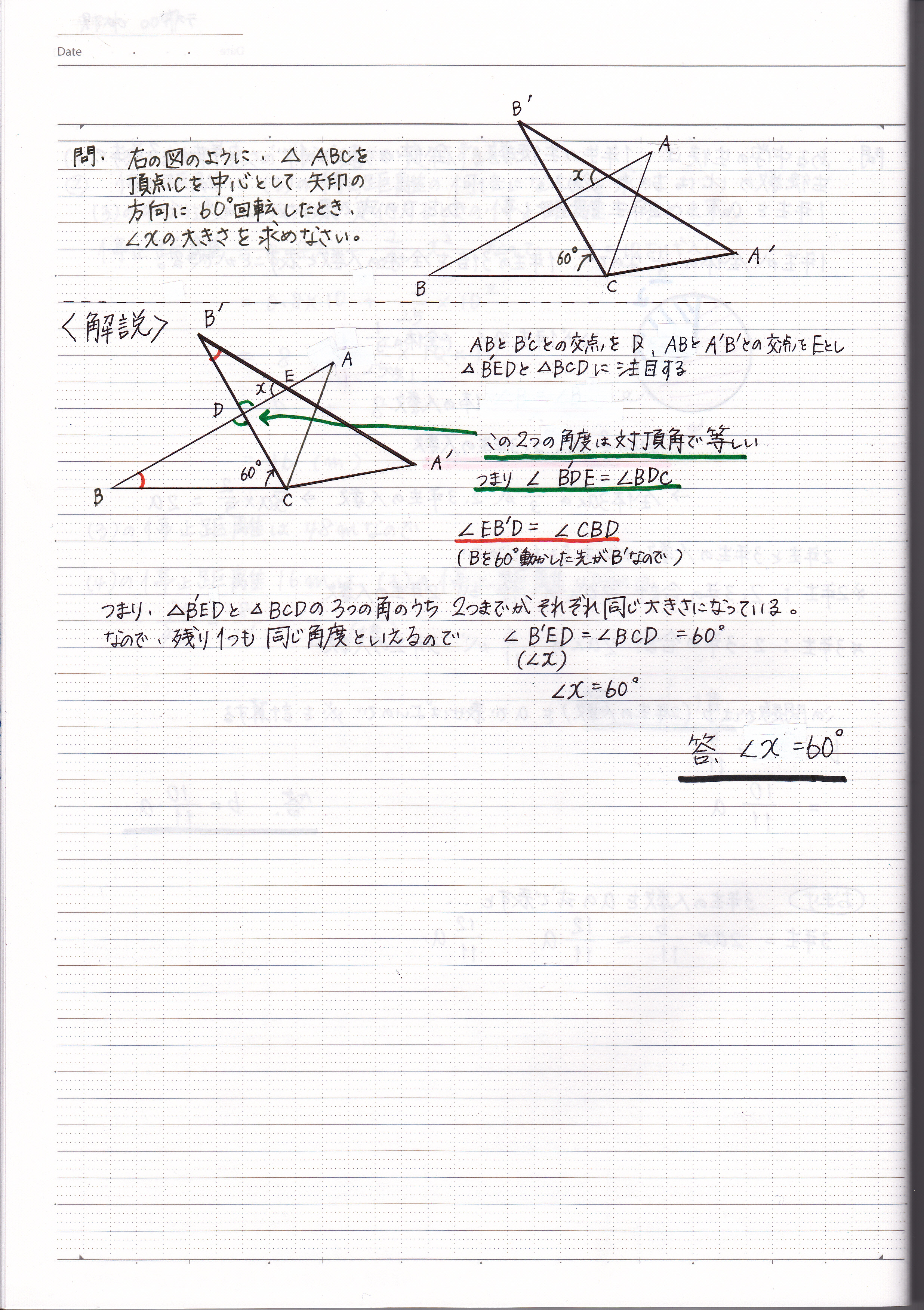



回転する図形の角度の求め方 現役塾講師のわかりやすい中学数学の解き方




余弦定理で角度を求める方法 数学の星



3




余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ




円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ




タンジェントとは何か 中学生でも分かる三角関数の基礎
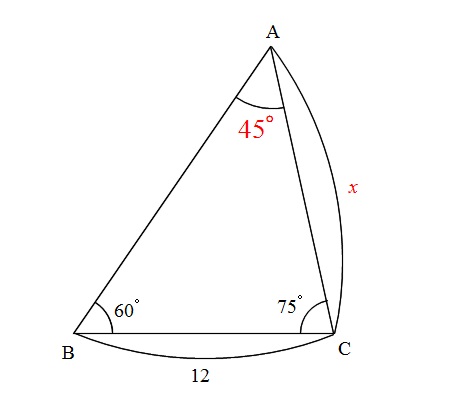



三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない




三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




三角形面積求め方 三角形とは 面積公式 角度 辺の長さ 重心 比の計 Jbqhd




簡単公式 平行四辺形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中2 数学 4 2 三角形の角度の利用 Youtube




三角形の辺や角が与えられたとき残りの辺や角を求める方法 数学の偏差値を上げて合格を目指す




角度の求め方を教えてください ちなみに答えは です お願いします Clear



紙ヒコーキ型図形の角度を求める 平行線と角 勉強ナビゲーター
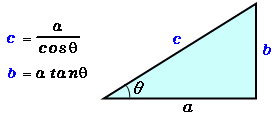



角度と底辺から斜辺と高さを計算 高精度計算サイト




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ
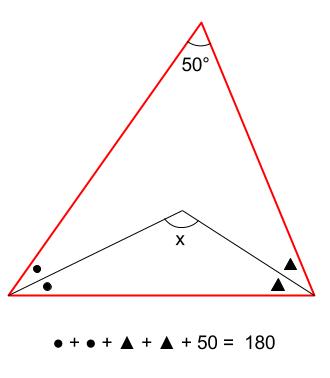



中学数学 求角と方程式 中学数学の無料オンライン学習サイトchu Su
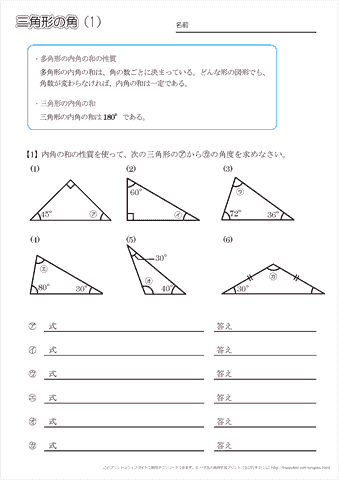



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生
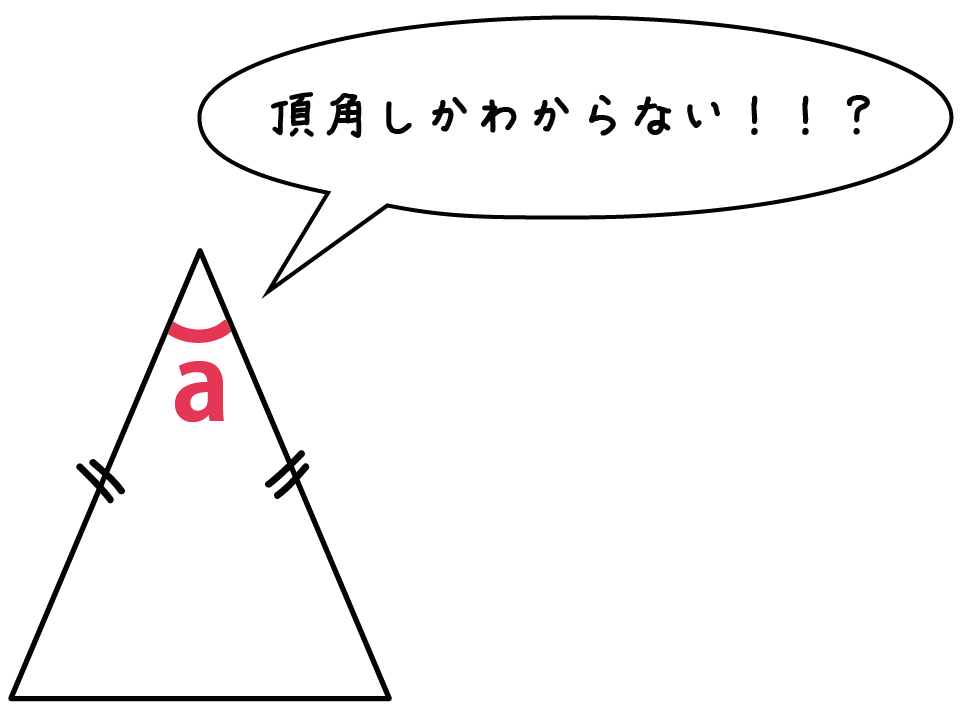



簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく
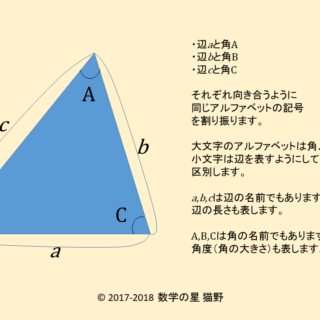



第2余弦定理の公式は辺と角度の関係を簡潔に表す 数学の星
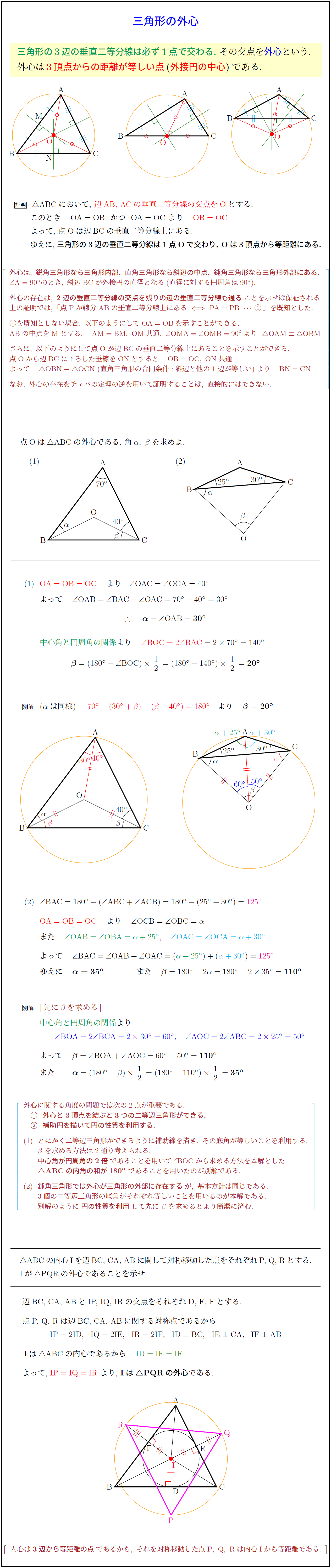



高校数学a 三角形の五心 三角形の外心とその存在証明 受験の月
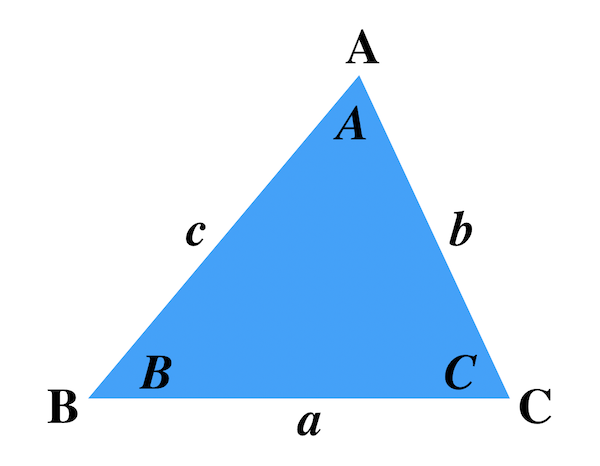



三角比 正弦定理と余弦定理を詳しく解説 スタディクラブ情報局



角度の求め方 算数の教え上手 学びの場 Com



直角三角形の角度の求め方 教えて下さい 斜辺以外の2辺の長さが分かっ Yahoo 知恵袋




三角形の辺から角度を計算 製品設計知識




Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算
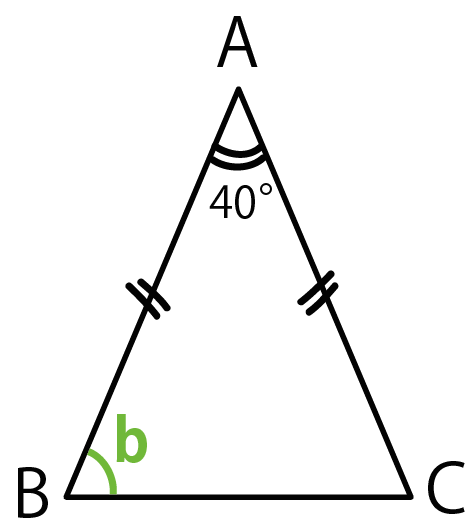



簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく




角度の求め方 角度の求め方 Mqttk




三角形の外心 高校数学a Youtube
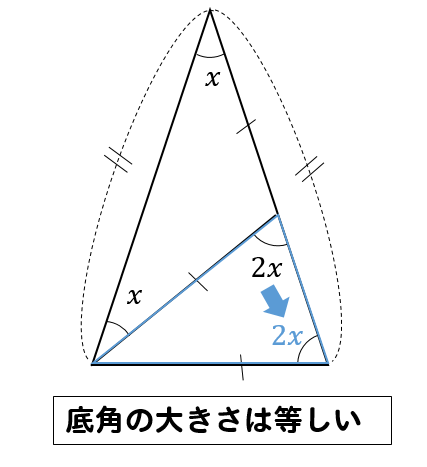



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ




三角形の外角と内角の公式 簡単な問題で 外角の求め方を理解しよう 中学や高校の数学の計算問題




底辺と高さから角度と斜辺を計算 高精度計算サイト




内心とは 三角形の内心の求め方や比の使い方 性質の証明 位置ベクトルをわかりやすく解説 遊ぶ数学




ヘロンの公式で三角形の面積を求める 三辺の長さがわかっているときはコレ 数学の面白いこと 役に立つことをまとめたサイト
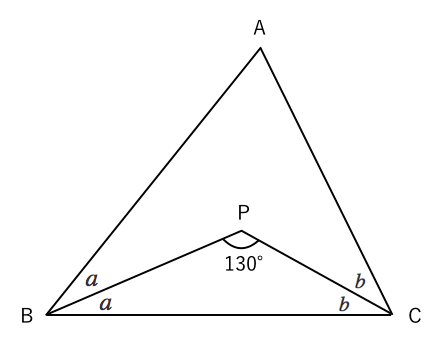



図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に
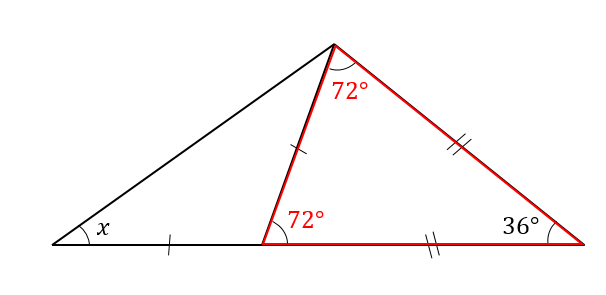



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ




角度の求め方 算数の教え上手 学びの場 Com




正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座




二等辺三角形の角を求める Youtube



1




あ かまでの角度を求めてください 急いでます 教えてください Clear
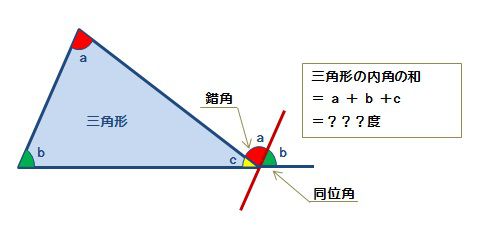



三角形の内角の和 算数の公式覚えてますか




数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




外角の求め方 外角の和を使って多角形の角度を求める問題 中学や高校の数学の計算問題




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ
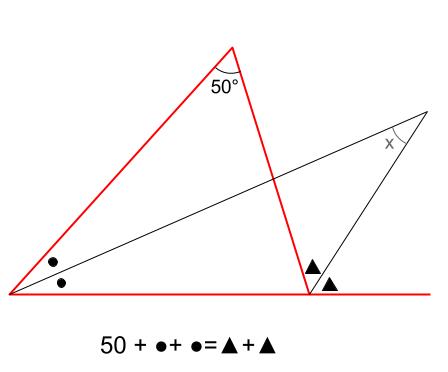



中学数学 求角と方程式 中学数学の無料オンライン学習サイトchu Su




二等辺三角形を使う角度計算です 一応解けたのですがもっと簡単な式があると思うので教え Clear




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ



3




正三角形や二等辺三角形の内角 Youtube




ブーメラン型の角度の求め方を解説 Youtube



0 件のコメント:
コメントを投稿