外側の正方形の面積はどうかな? 半径10cmの円の外側に、正方形をかいて 円の面積のおよその大きさを考えよう 半径10cmの円の外側に正方形を書くと → 上の図のように、円の面積は、1辺10cmの正方形4つ分の面積より小さいことに気づかせます。正多面体の頂点の数 つづいて正多面体の頂点の数です。 結論から言うと以下の公式で求められます。 (頂点の数)=(面の頂点の数)×(面の数)÷(1点に集まる面の数) たとえば正四面体について考えてみましょう。 面の形は正三角形なので「面の影片:例題正方形的周長公式,數學 > 主題式 > 國小 > 數與量 > 面積 > 四年級周長與面積。源自於:均一教育平台 願 每個孩子都成為終身學習者,成就自己的未來。
这样学习长方形的面积 不用老师教 学生也能记忆犹深
正方形面積公式 對角線
正方形面積公式 對角線-正方形 面积 = a 2 a = 边长 矩(长方)形 面积 = 宽 × 高 w = 宽 h = 高 平行四边形 面积 = b × h b = 底 h = 垂直高度 梯形 面积 = ½(a b) × h h =垂直高度 圆形 面积 = π × r 2 周长 = 2 × π × r r = 半径 椭圆形 面积 = π ab 扇形 面积 = ½ × r 2 × θ r =半径 θ=角度(以弧度 正方形的面积等于边长的平方:S=a*a,也就是边长乘以边长。 已知正方形面积S,要就正方形边长,方法为 边长a²=S a=根号S 例:已知正方形面积为16,求正方形边长 a²=16 a=4 扩展资料 另一种正方形面积计算公式 正方形面积=对角线×对角线÷2 S=对角线×对角



正方形面积对角线公式正方形面积的对角线公式是什么 天奇生活
方形と正方形の面積) B① C① D② 展 4 長方形や正方形の面積の公式を使えるように 複合図形を補助線で分けたり、図形を補ったりし て、面積の求め方を考える。 ・複合図形の面積の多様な求め方を理解すること。 (本時)面積:物體的表面—平面圖形的大小。 體積:物質或物體所占空间的大小或占據一特定容積的物質的量。 計算公式 面積 長方形面積=長×寬 = 正方形面積=邊長 2 = 平行四邊形面積=底×高;$$正方形=1辺\times 1辺$$ $$長方形=たて\times よこ$$ $$平行四辺形=底辺\times 高さ$$ $$ひし形=対角線\times 対角線\times \frac{1}{2}$$ $$台形=(上底下底)\times 高さ\times \frac{1}{2}$$ 〇 底面積は四角形の種類によって、面積の公式を使い分けてね!
角パイプ 面積計算 公式 求め方 正方形 長方形 縦 横 厚さ 厚み 自動 area 正方形の面積は、 a^2/2 で計算できちゃうよ。 つまり、 (対角線の二乗)÷2 ってわけだね。 たとえば、 対角線BDが10cmの正方形ABCDがあるとしよう。 この正方形の面積の求め方は、 (対角線)×(対角線)÷2 = 10×10÷2 = 50cm^2 になるんだ。 どう?? 公式正方形の面積を求める公式は 正方形の面積 = 一辺 × 一辺 なので、正方形の面積を S とすると S = 4 × 4 = 16 ( c m 2) になります。 次は一辺の長さが小数点を含む正方形の面積を計算します。
正方形の面積を求める2つの公式 具体例で学ぶ数学 > 図形 > 正方形の面積を求める2つの公式 最終更新日 ~公式その1~ 1辺の長さが分かっている正方形の面積は (1辺)× (1辺) または (たて)× (よこ) で求めることができる。 ~公式その2~(解説) (1)← すなわち の展開を行うには,右図のように「総当たり」になるように順に掛けて,できた項を足します. ≪この公式の図形的な意味≫ 右図のような1辺の長さが である正方形の面積 は 展开全部 一、正方体的体积公式:棱长×棱长×棱长 或 棱长的立方; 字母表达式:a×a×a 或 a的立方。 二、正方体表面积公式:S=6×(棱长×棱长) 字母表达式:S=6a² 正六面体(正方体)具有如下特征: (1)正六面体有8个顶点,每个顶点连接三条棱。 (2




I2 Hdslb Com Bfs Archive D2f9b4bca51c8dc0dfbafd




怎么计算正方形的周长 最有妙招网
ゆったり座れる木目調のベンチ。ミヅシマ スクエアベンチ 正方形 ベランダなど大面積ベンチ 間口1246×奥行1246×高さ400mm三角形の面積 ・正三角形の面積 1辺の長さを指定して、正三角形の面積を計算します。 ・三角形の面積(底辺と高さ) 底辺と高さから三角形の面積を計算します。 ・三角形の面積(2辺と間の角度) 2辺と間の角度から三角形の面積を計算します。 若S为正方形的面积,C为正方形的周长,a为正方形的边长,v为正方形的对角线,则: 正方形的判定定理 1、对角线相等的菱形是正方形。 2、有一个角为直角的菱形是正方形。 3、对角线互相垂直的矩形是正方形。 4、一组邻边相等的矩形是正方形。



正方形面积公式小升初数学题求正方形面积 长方形和正方形的公式



梯形面积公式换算 梯形形面积计算公式梯形形的面积公式三角形梯形面积公式 尚书坊
正 方 體 有 6 個 面 , 每 一 個 面 都 是 正 方 形 , 且 其 面 積 都 一 樣 大 。 所以表面積= = = 。 所 以 表 面 積 = 5 × 5 × 6 = 25 × 6 = 150 。 答: 平方公尺。 答 : 150 平 方 公 尺 。 寫成公式為: 寫 成 公 式 為 : 正方體表面積=邊長 邊長 🔊 Play The area of a parallelogram is its base times its height 平行四辺形の面積は、底辺×高さです 🔊 Play The rectangle is 4meter wide and 3meter height long その長方形は、幅4メートル 高さ3メートルです 🔊 Play The interior angles of a planar quadrilateral add up to 360 degrees 四角形の内角の角度をすべて足すと、360度になり 長方形の面積は,「たての長さ」×「横の長さ」で求められると考えてよいのでしょうか。 長方形の面積=たての「数」×横の「数」と考えます。 面積は,図形を敷き詰めた単位正方形のいくつ分かの数で表します。 単位正方形\(e\)



正方形面积对角线公式正方形面积的对角线公式是什么 天奇生活
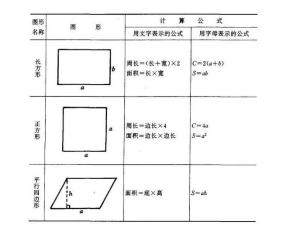



面积公式 搜狗百科
〇面積の単位㎠を知り、1㎠を単位にしていろいろ な形の面積を求めたり、方眼紙上でつくったりす る。 〇長方形や正方形の面積を求める公式を考え、公式 を適用して面積を求める。 既習事項(長さやかさ)とのつながりを意識させ、面積三角形 (さんかくけい) の 面積 (めんせき) の求め方の 基本 (きほん) は「 底辺 (ていへん) × 高 (たか) さ ÷ 2」ですが、高さが分からないときに 他 (た) の 情報 (じょうほう) から面積を求める 公式 (こうしき) がいくつもあります。 ここでは、三辺の長さが分かっている 場合 (ばあい) や、 角度 たとえば、「2つの対角線の長さが 4 c m, 7 c m の平行四辺形」の面積は 4 × 7 ÷ 2 = 14 c m 2 となります。 ひし形の面積の公式は 「たての対角線の半分の長さ」と「横の対角線の半分の長さ」の直角三角形の4倍 と考えると分かりやすいです。 「たての対角線




正方形面積 Youtube




例題 長方形面積公式的應用 數學 均一教育平台
正方形是特殊的平行四边形,也是特殊的长方形。在同一平面内:四条边都相等且一个角是直角的四边形是正方形 3 。 有一组邻边相等的矩形是正方形。 有一个角为直角的菱形是正方形。 正方形对角线相等練習 次の図形の面積を求めましょう。 ① 式 6×6=36 答え 36㎠ ② 式 2×8=16 答え 16㎠ ③ 式 4×2=8 答え 8㎡ 正方形・長方形の面積(1) 年 組 番名前 学習日 月 日 広さのことを面積と言います。 面積は、1辺が1㎝の正方形がいくつ分あるかで表します。正三角形の面積 三角形の面積(底辺と高さから) 三角形の面積(2辺と夾角から) 三角形の面積(3辺からヘロンの公式) 三角形の面積(1辺と2角から) 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積(4辺の長さから)




正方形的面积公式是什么 正方形面积算法 合抱木装修网



图文版 小学数学图形的周长 面积 体积公式 小学 香蕉教育网
正方形 正方形 (英文叫 square )係 幾何圖形 ,係 正多邊形 一種。 佢係 四邊形 ,有四條一樣長嘅 邊 ,同埋又係 四角形 ,有四隻 角 ,四隻都係 直角 。 如果正方形四隻角叫甲乙丙丁, 甲乙丙丁 。 睇斜正方形 正三角形 薄肉中空円 薄肉中空矩形 薄肉I形 薄肉I形弱軸 2 3 4 R 3 4 4 1 2 1 A f ・ H f + トの A w ・ H f 4 1 A f ・ H + A ・ H f T 6 2 2 - 2 1 B ・ T f (H - T f) 2 + (H - 2T f) 2 T w R 2 (H - 2T f - R) 4 1 4 1 1 0 c 1 0 c 2 A f : 片側フランジプレー トの 断面積 A正多角形の面積公式一覧と導出方法を解説正二十四角形まで 21年1月28日 1辺の長さaの正方形の面積は、もちろん a 2 ですが、正三角形の面積公式は知っていますか 中学や高校の試験で登場するため、正三角形の面積公式は覚えておいて損はありませ〇面積の単位㎠を知り、1㎠を単位にして




正方形怎么算面积公式 正方形的面积怎么算 三人行教育网 Www 3rxing Org




面积公式 搜狗百科
ひし形の面積 平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積正方形の面積が分かっているとき、辺の長さは簡単に求められます。 a=√A です。正方形の面積がA=a^2なので、ルートをとれば1辺の長さが逆算できます。 まとめ 今回は正方形の面積について説明しました。簡単な公式で計算できます。求積公式(平面) a=面積 正方形 長方形 平行四辺形 備考 a寸法はb辺に対し直角に測ったもの 直角三角形 a=面積 鋭角三角形 鈍角三角形 台 形 不平行四辺形 なお点線にて示すごとく二つの三角形となし、各々の面積を計算し、
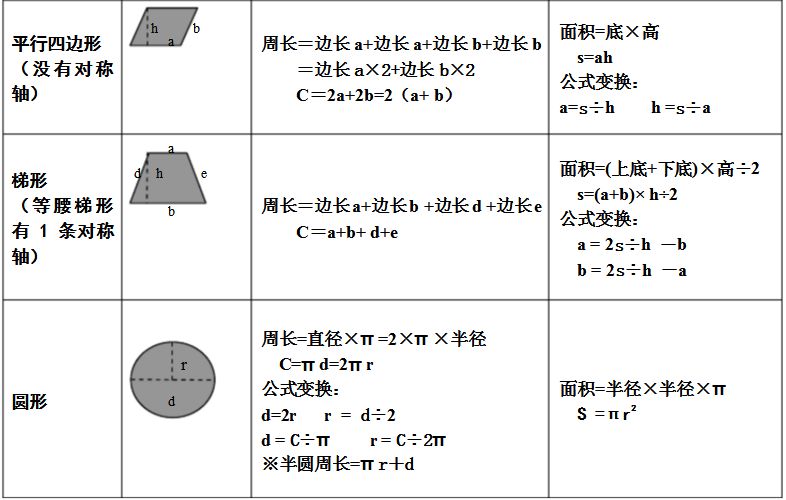



计算长方形的周长和面积公式 三年级数学上册长方形正方形计算公式及练习 附图形计算公式表 偷得一寸光的博客 Csdn博客



长方形与正方形面积计算 四 面积计算 奥数网
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators



面积公式 搜狗百科
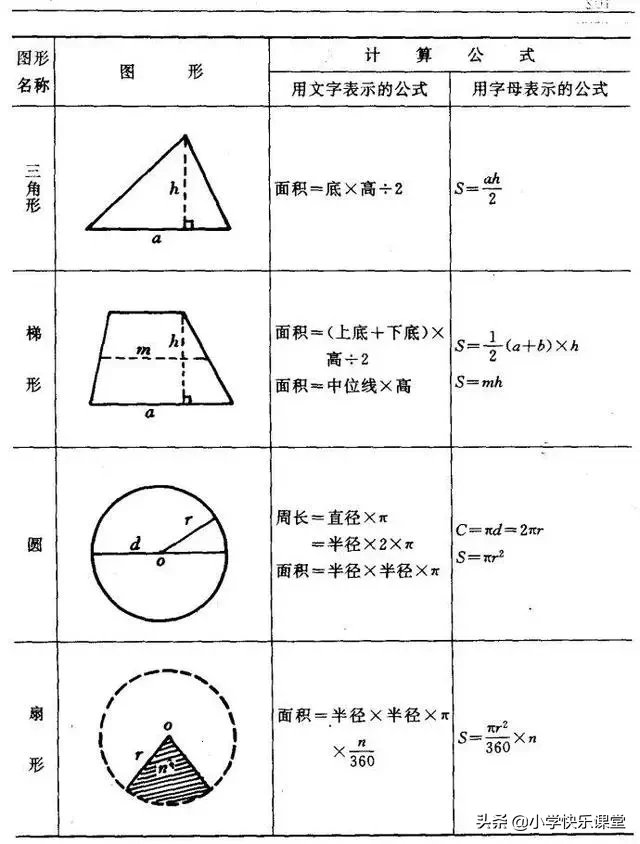



小学生正方形的面积公式



不规则正方形面积公式 西瓜视频搜索



正方形面积公式 搜狗图片搜索




正方形周长和面积公式是什么小学正方形的周长是 制作蛋糕
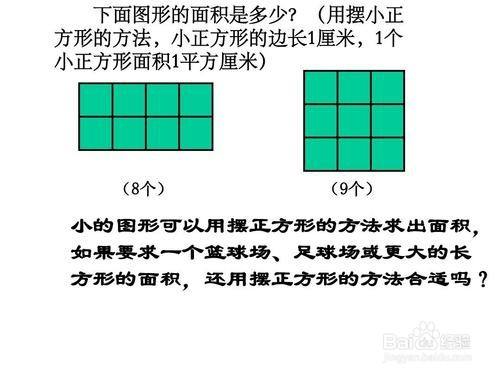



长方形的面积公式是怎么得到的 百度经验




平面圖形的面積公式flashcards Quizlet



不规则正方形面积公式 西瓜视频搜索




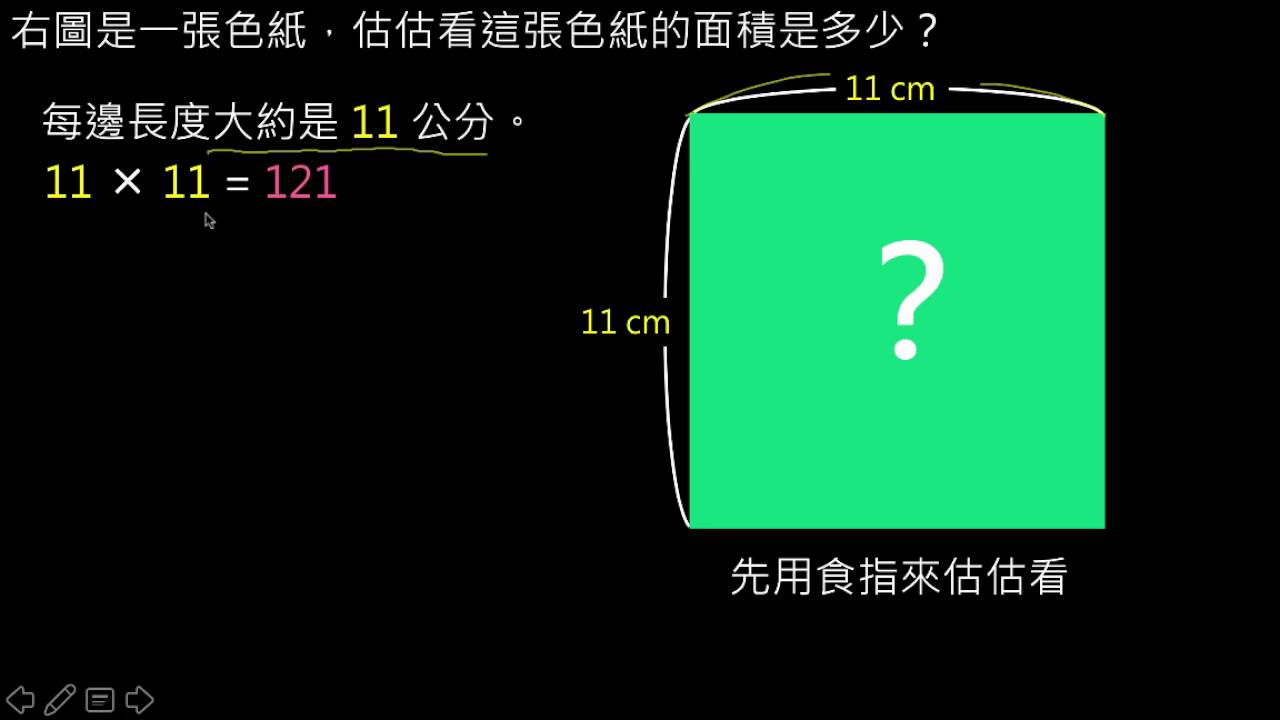
例題 正方形的周長公式 數學 均一教育平台




怎么利用对角线的长度求正方形的面积 最有妙招网




3种方法来计算正方形的面积



正方形的面积公式字母 搜狗搜索



Q Tbn And9gcs4mf4ga4ivcw9oaofx1 Zkqgkhy6m1tx85ng7ya0kcksl0rfiq Usqp Cau



正方形面积公式1 5年级 西瓜视频搜索




呈分試數學科必睇 圖形題目重點溫習攻略 公式 題目 學而思香港



长方形 正方形面积的计算 面积ppt课件下载 第一ppt



面积怎么算面积的计算方法 天奇生活




正方形的周长公式 长方形正方形面积和周长的公式 三人行教育网 Www 3rxing Org




3种方法来计算正方形的周长




数单位正方形求面积计算公式 视频 长方形 正方形面积的计算 可汗学院




3种方法来计算正方形的周长



1




05 正方形的面積公式 Youtube



面积公式 毛毛情感吧
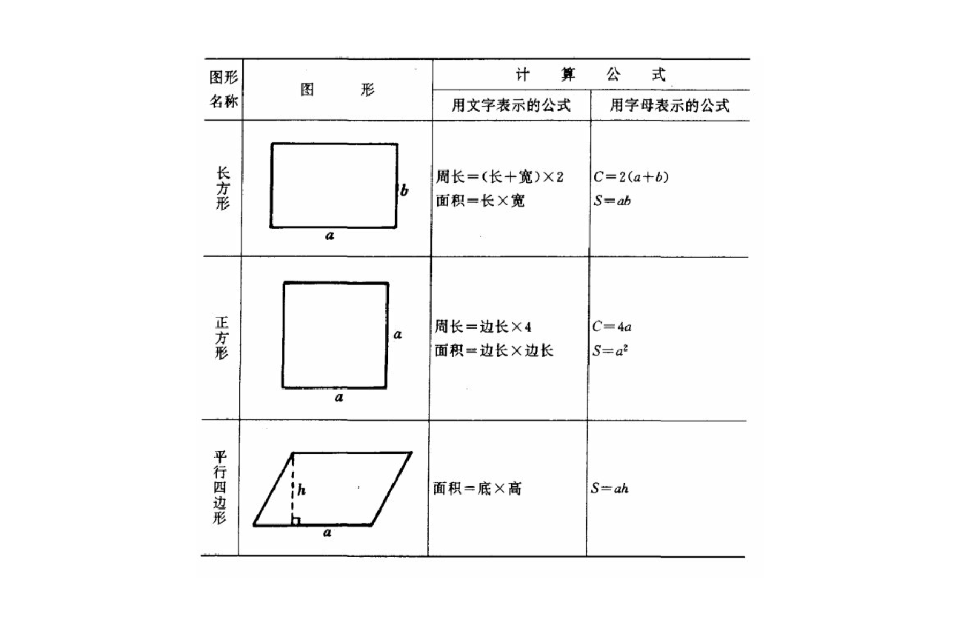



面積公式 常見面積定理 圓公式 扇形公式 圓環面積 三角形公式 海倫公式 坐標公式 中文百科全書




06 正方形面積公式的應用 Youtube




基礎 長方形 正方形的面積公式 數學 均一教育平台



正方形面积公式小升初数学题求正方形面积 长方形和正方形的公式



梯形面积公式计算公式 梯形面积计算公式的推导 教学设计 尚书坊



不规则正方形面积公式 西瓜视频搜索



正方形怎么算平方面积长方形 三角形 正方形面积公式怎么算



Q Tbn And9gcrxrw7 Um5jpuzzqblohrmzui Zwisxv7jrpthk1fc4mcyvocgy Usqp Cau
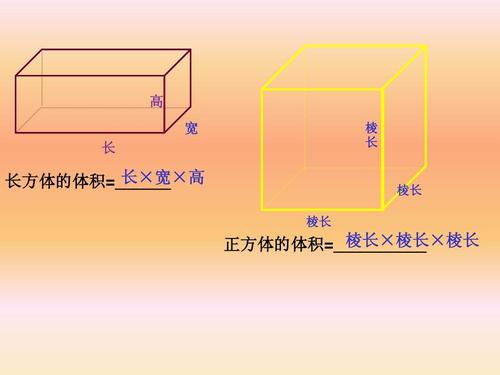



正方体面积计算公式 正方体的体积公式和正方体的表面积公式 作业帮




长方形正方形的面积 Youtube




03 長方形的面積公式 Youtube




正方形的面积公式是什么 正方形面积算法 合抱木装修网



圆面积公式计算正方形面积计算公式正方形面积的计算公式是什么 尚书坊



Q Tbn And9gctn9tlpkqkzba6gjqjpmar6ixda9syxh1lq6mu5uvmgrxge1bsg Usqp Cau



三年级长方形与正方形面积练习题及答案 巧求周长 奥数网




正方形周长公式用字母表示怎么算的面积公式 小街网




I2 Hdslb Com Bfs Archive 110f0f3cde6ca694a465



正方形面积对角线公式正方形面积的对角线公式是什么 天奇生活



图文版 小学数学图形的周长 面积 体积公式 香蕉教育网



正方形面积公式 表情大全




正方形等各种图形的面积公式集合 百度经验




Ct 974dfm6qgsm



06 正方形面積公式的應用 Youtube




Amc 10 第一讲 数学中的面积公式都是怎么来的 知乎




图形面积周长公式第1页 驾考预约大全



正方形面积公式 长方形和正方形面积计算 教学反思 学习岛



正方形双龙提梁百宝箱 腾讯视频



正方形面积公式和周长 西瓜视频搜索



圆形 三角形 正方形 矩形 平行四边形 梯形和扇形的面积
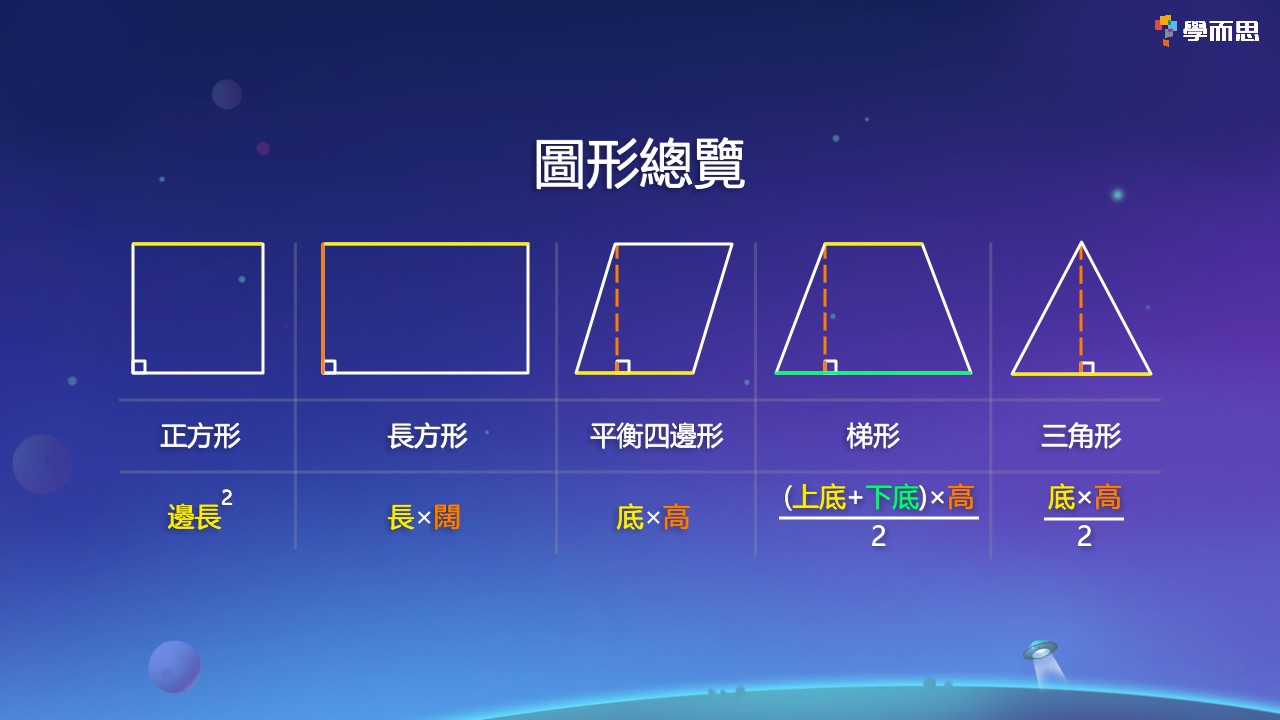



呈分試數學科必睇 圖形題目重點溫習攻略 公式 題目 學而思香港
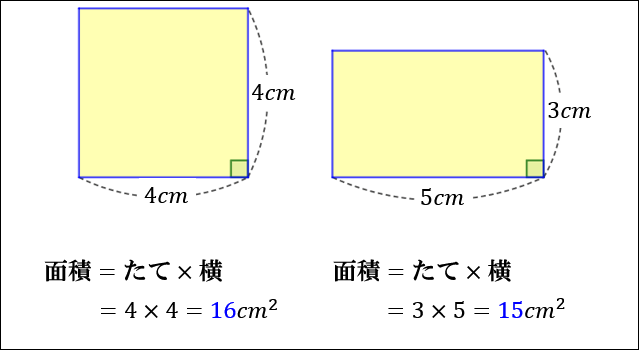



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ




4年级006 基本直线型面积公式正方形与长方形面积计算 Youtube




长方形周长的公式是什么




簡単公式 正方形の面積の2つの求め方 Qikeru 学びを楽しくわかりやすく



正方形面积公式 长方形和正方形面积计算 教学反思 尚书坊



Data Wuyouwenku Com File Convert 21 03 24 14



正方形面积公式和周长 西瓜视频搜索



弧长及面积公式 腾讯视频




正方形内求圆面积公式




I2 Hdslb Com Bfs Archive af499
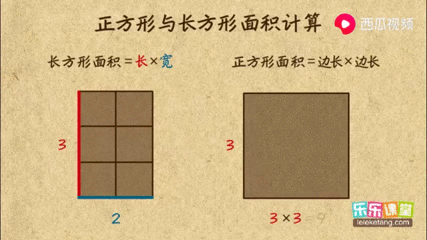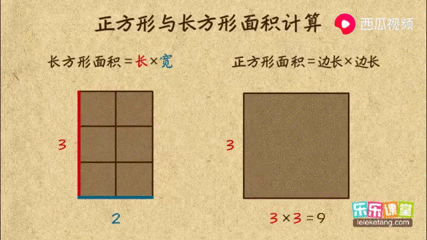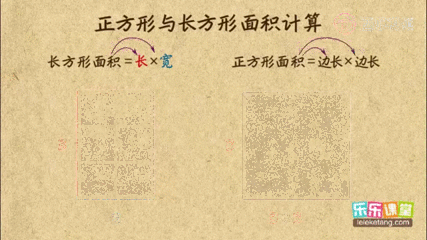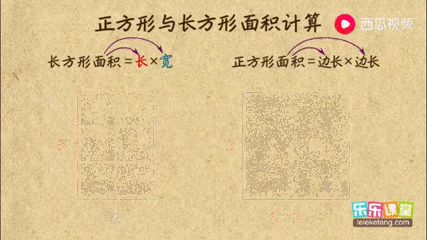



正方形面积公式怎么算 搜狗搜索



这样学习长方形的面积 不用老师教 学生也能记忆犹深



技巧 数学图形面积计算的十种方法 正方形



长方形和正方形的面积计算课件3 人教版小学数学三年级下册课件 小学课件 中国儿童资源网



正方形面积公式及判定定理 扒拉扒拉




3种方法来计算正方形的周长




Amc 10 第一讲 数学中的面积公式都是怎么来的 知乎




长方形和正方形面积的计算ppt课件下载 找资源 101教育ppt



非常規圖形求面積的10大方法 圖文並茂超易懂 雪花新闻




活動二 正方形面積公式 台南市育成專案四年級數學




正方形公式第1页 驾考预约大全



正方形的面积公式 生活常识
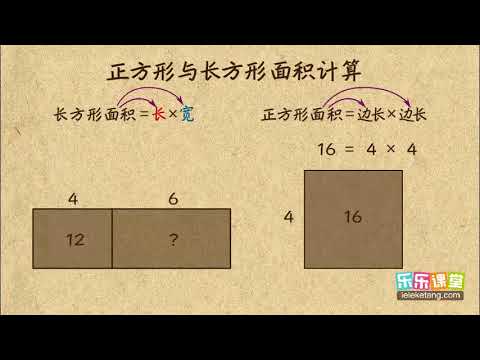



29 1 正方形 长方形面积计算小學奧數四年級幾何 Youtube



长方形的面积怎么算 360新知



小学数学图形的周长 面积 体积公式 孩子学习必备 周长 体积 圆柱 新浪新闻




小升初数学必会的10种图形求面积解题法 经典收藏版 最全汇总 每日头条



正方形面积公式是什么



正方形长方形面积公式 搜狗图片搜索



小学数学升学考试必备题型 求正方形面积 公式熟练运用就简单 网易视频




正方形面積計算公式 正方形的面積等於邊長的平方 S A A 正方形面積計 百科知識中文網




正方体的表面积公式是什么得六个面的面积总和为长



正方形面积公式1 5年级 西瓜视频搜索



正方形面积公式是什么 万图壁纸网




小學所有的數學 圖形的計算 公式 每日頭條




正方形的面积公式文字 正方形的面积公式 三人行教育网 Www 3rxing Org




05 正方形的面積公式 Youtube



0 件のコメント:
コメントを投稿