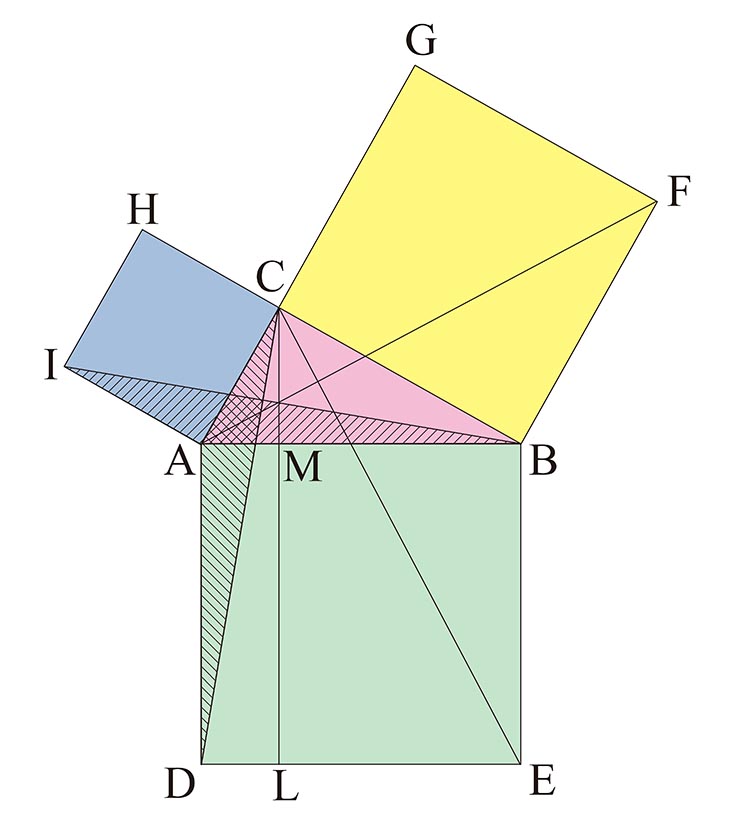
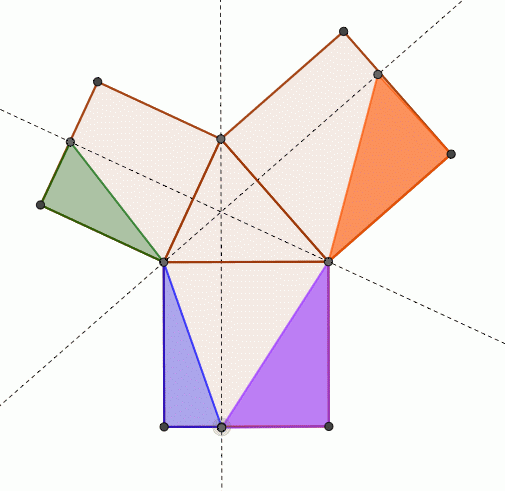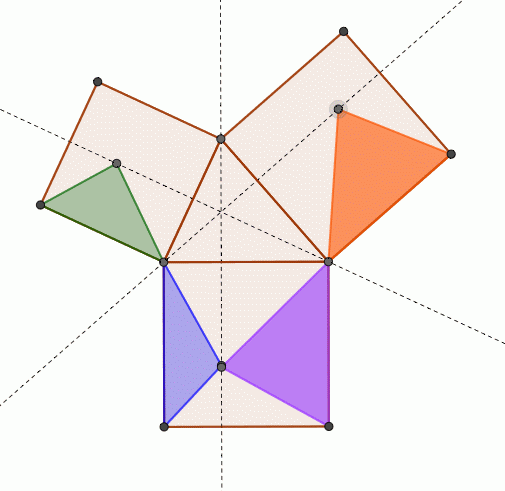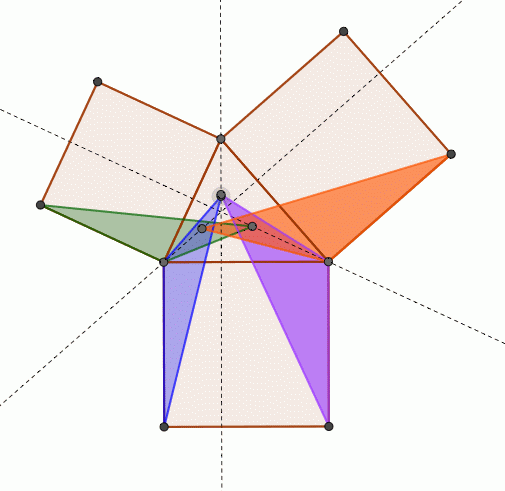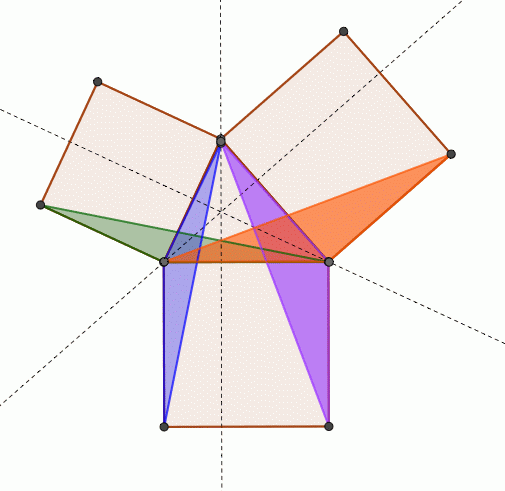
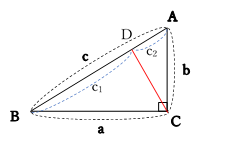
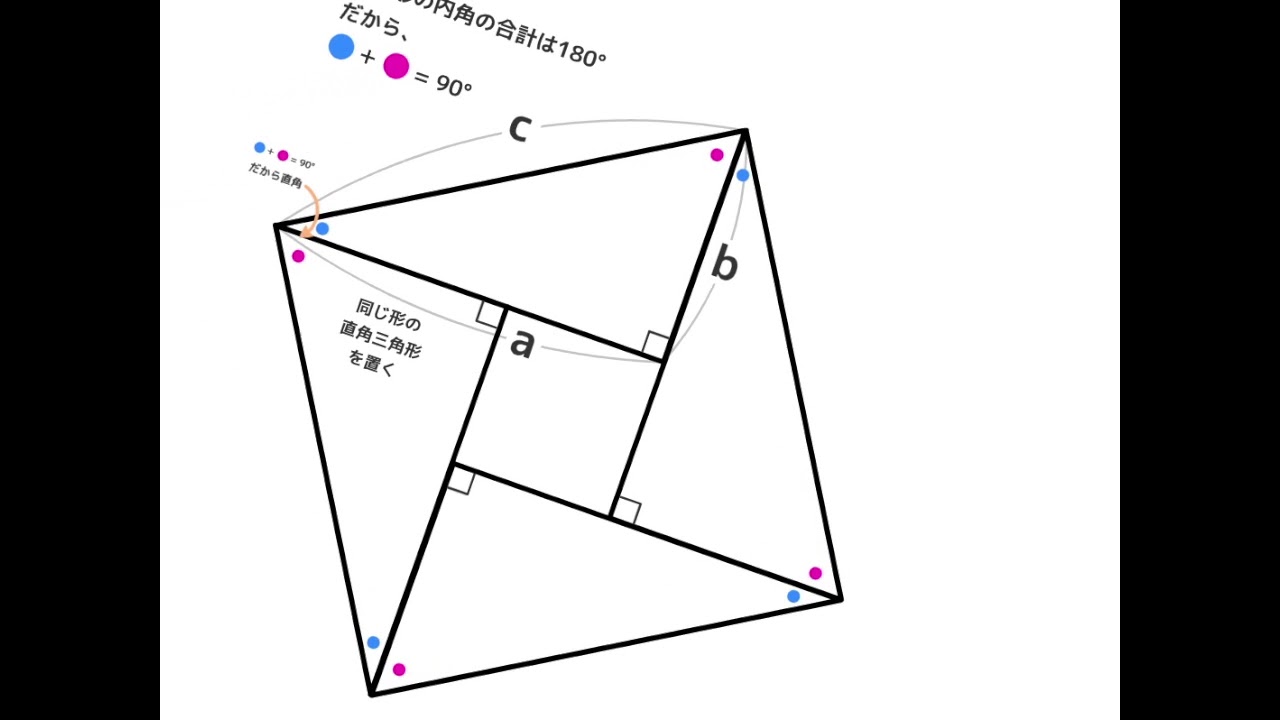
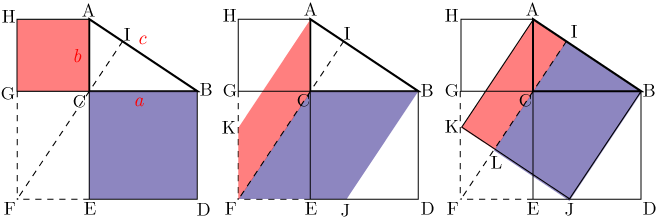
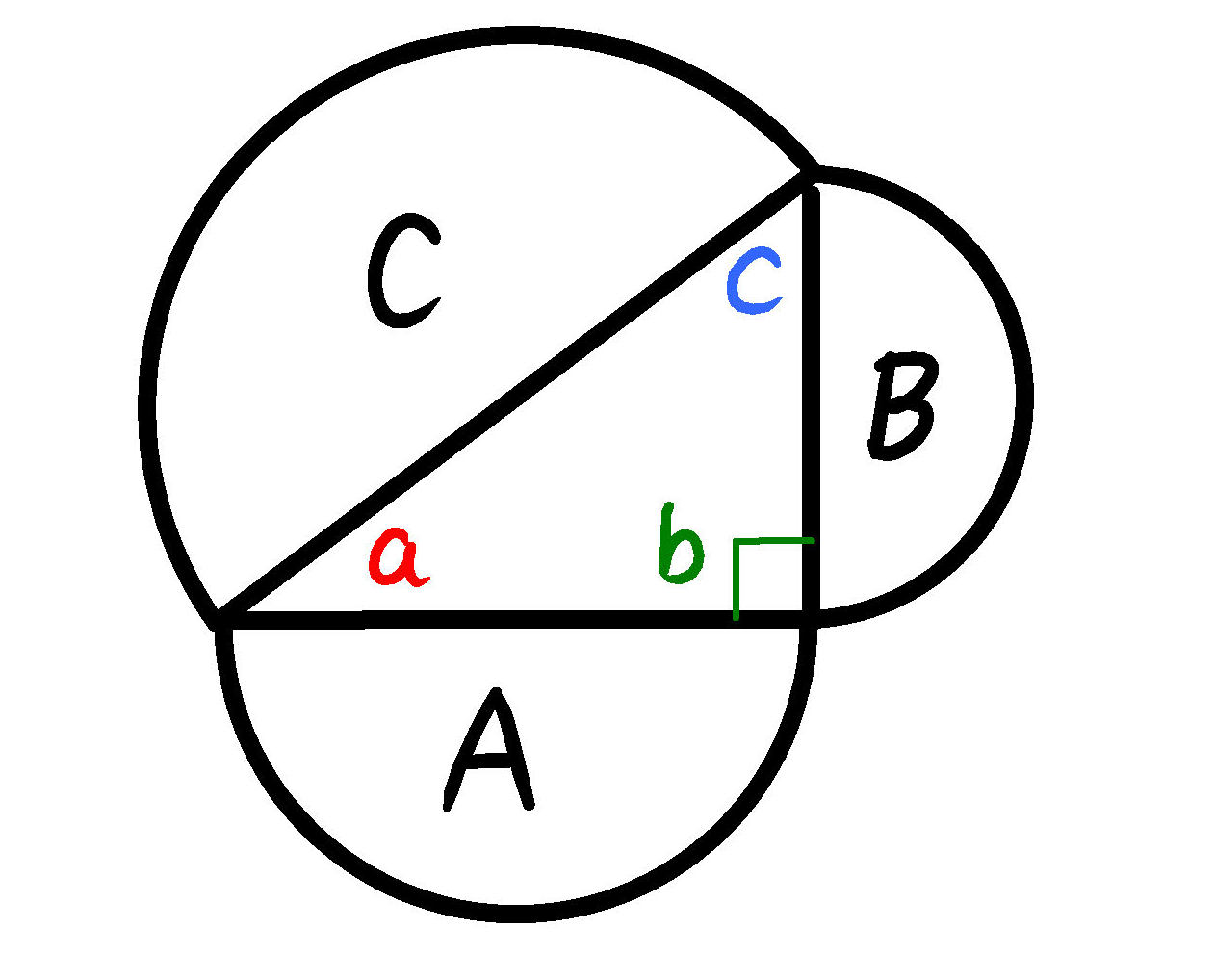
三角比の導入 三平方の定理について 三平方の定理の証明方法は非常にたくさんある 等積変形を用いた証明法は以下の通り 下の画像をクリックすると動画が表示されます それでは 以下の図を利用して 三平方の定理の別証明を考えてみよう
斜辺の平方は他の2辺の平方の和 が最も優れているだろう。 昨今の生徒の意識として、結果さえ覚えればOKで、その成り立ち等に関心を払わない 場合が多い。 このピタゴラスの定理（三平方の定理）の証明は、百以上知られている。 が成り立つという有名な定理です ここでは, 三平方の定理 (平面上の定理)を3次元に拡張した, 四平方の定理を紹介します 定理 3つの面が直角三角形で, 1つの頂点に直角が集まっている三角錐を考えるとき, 直角三角形の面の面積を S1,S2,S3 S 1, S 2, S 3, 残りの
3平方の定理 証明 いろいろ
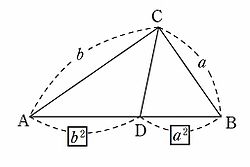
3平方の定理 証明 いろいろ-例3 右図で AC の長さは三平方の定理で求められるが， さらに相似図形の性質を使えば， ACBC=ABx になるので， x が求められる． （相似図形の性質をまだ習っていないときは こちらを先に 読む） 直角三角形 ABC に三平方の定理を適用すると 2152=AC2 AC2 四平方の定理とはひとことでいうと三平方の定理の3次元空間バージョンです． そう，四平方の定理はかの有名な三平方の定理さんと親戚のような関係なんです笑． 三平方の定理だと， $${ a }^{ 2 }{ b }^{ 2 }={ c }^{ 2 }$$ ですが四平方の定理だと，
ピタゴラスの定理 Wikipedia
4 k 3 4k3 4k 3 型の素数の指数が全て偶数 高々2つの整数の二乗和で表される整数はどんなものか？ という疑問に答える非常に有名な定理です。 この定理を知っていることで数学オリンピックで有利になることはないと思いますが，整数論の様々な知識を1番重要なこと 30°、60°、90°の直角三角形 では辺の比は必ず 12√3 になります!ラグランジュの4平方の定理よりすべての自然数は4つの平方数の和であらわすことができたので、 n 169 = a 2 b 2 c 2 d 2 (a、b、c、d = 0、1、2、3、) とあらわすことができる。しかし、この a、b、c、d の中に0を含んでいる場合がある。> つまり、
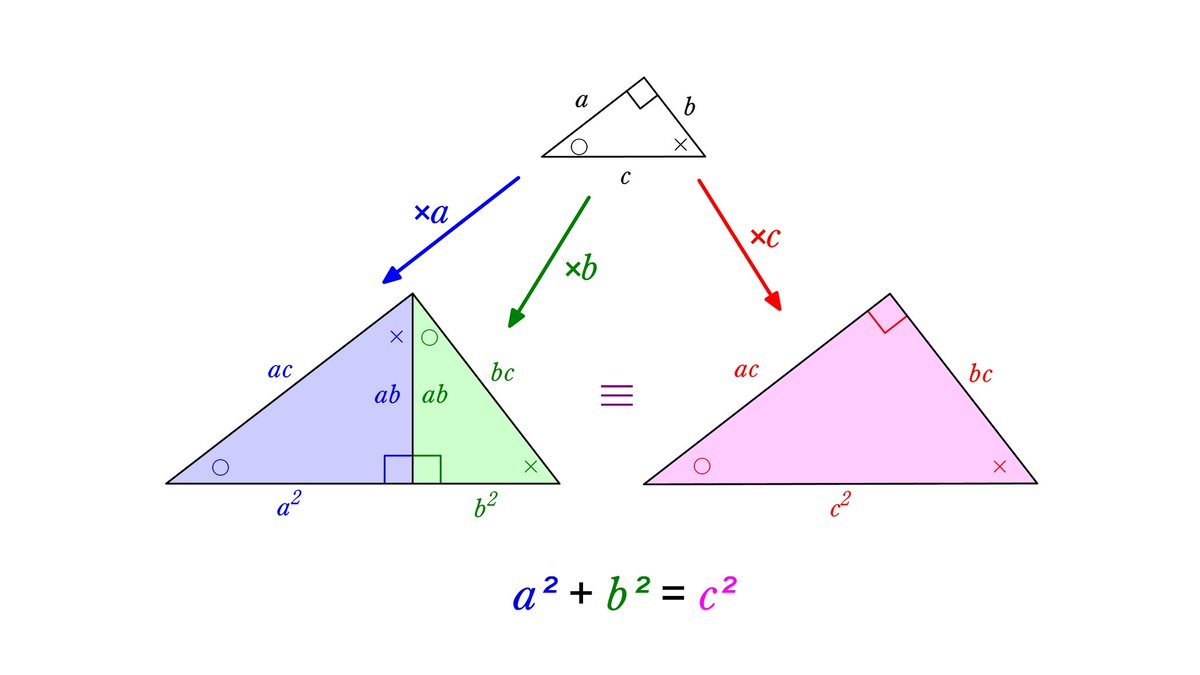
三平方の定理の逆とは、三角形の3辺がa² b² = c² を満たせば、その三角形は直角三角形であるというものです。図形の証明問題などに使われる場合があるので、覚えておきましょう。 三平方の定理の 三平方の定理の証明は問題として出題される可能性がありますので、一通り理解しておくと良いですよ。 直角三角形の角度と辺の比暗記 三平方の定理をもっと使いこなしていくために、下の \(\bf{4}\) パターンの直角三角形の角度と辺の比 を覚えましょう。回答 (3件中の1件目) 英語でよければ、 Pythagorean Theorem に大量に紹介されています。初等幾何学による類似のアプローチがほとんどですが、色々な図が楽しいです。 ただこういった基本的な事柄の証明は、ちょっと変わったことをしようとするとすぐ循環してしまい、「変わったこと」の材料を
3平方の定理 証明 いろいろのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 | 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 | 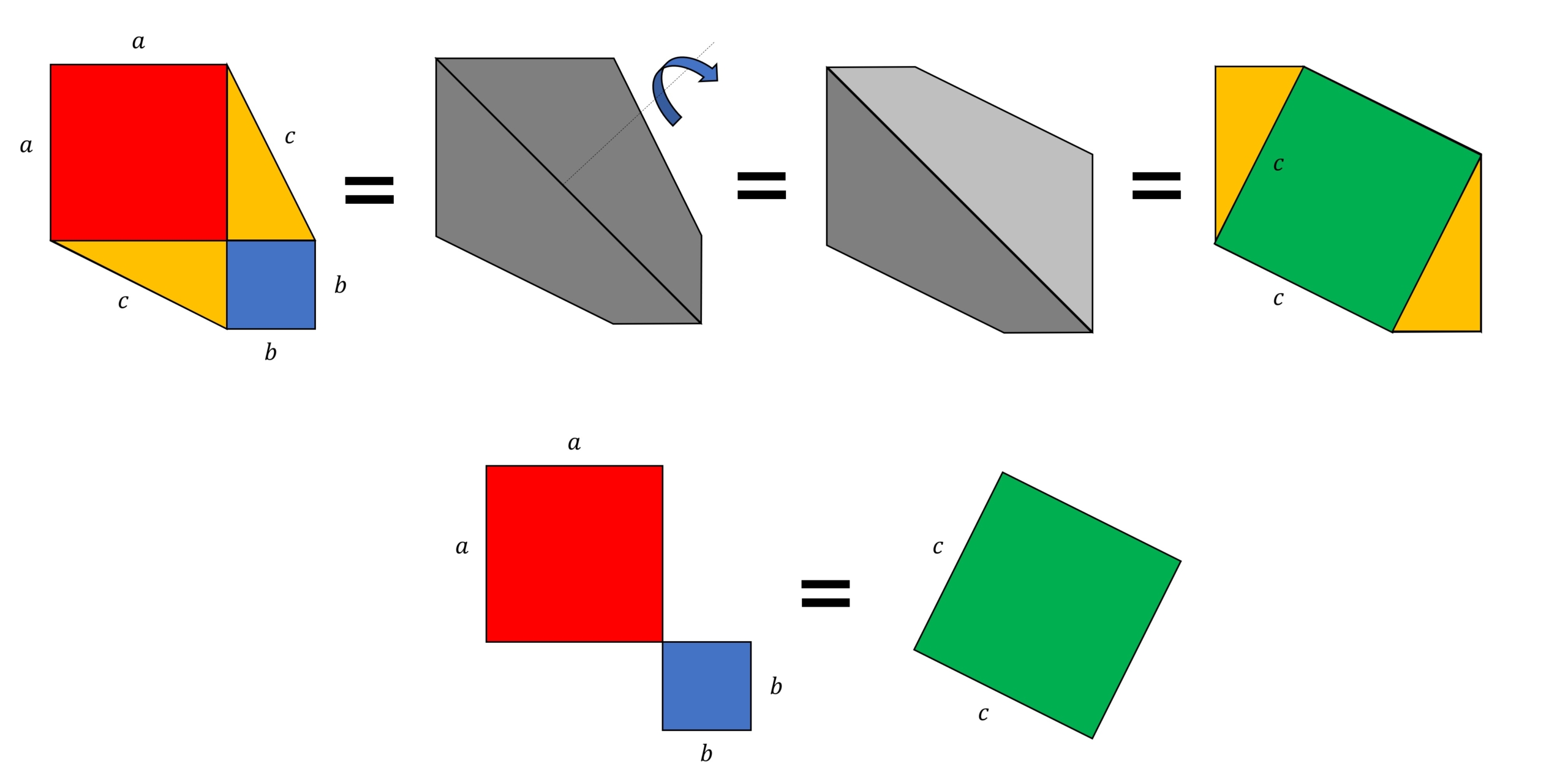 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 | 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 | 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 | 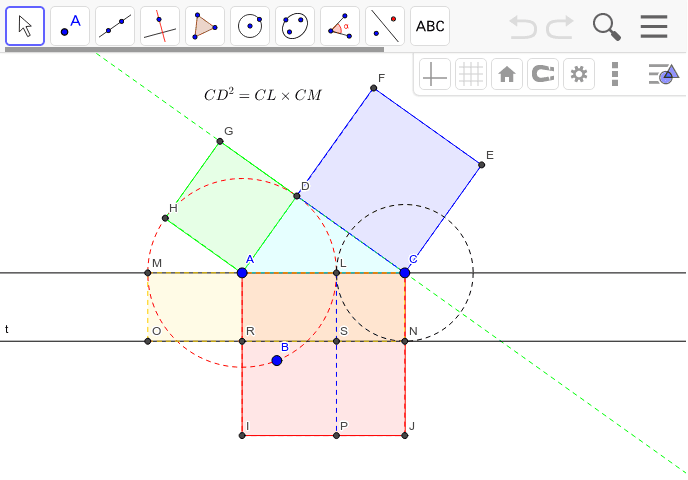 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 | 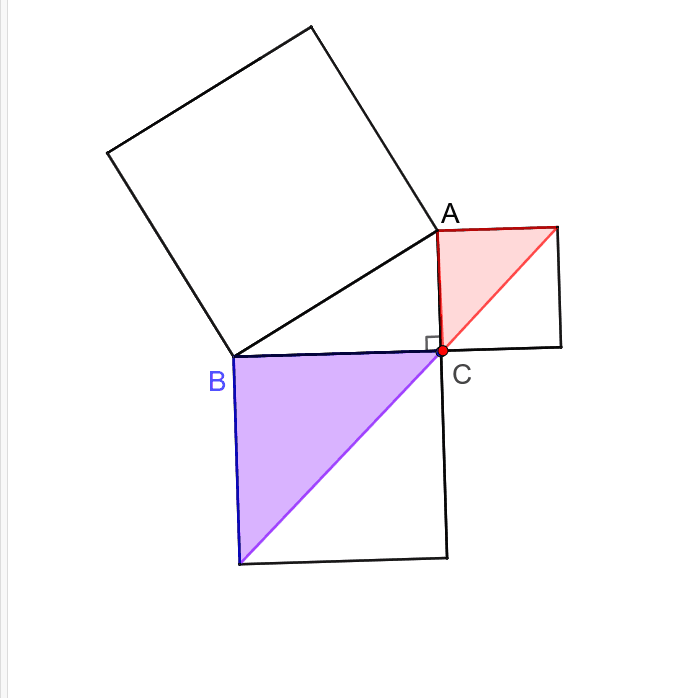 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 | 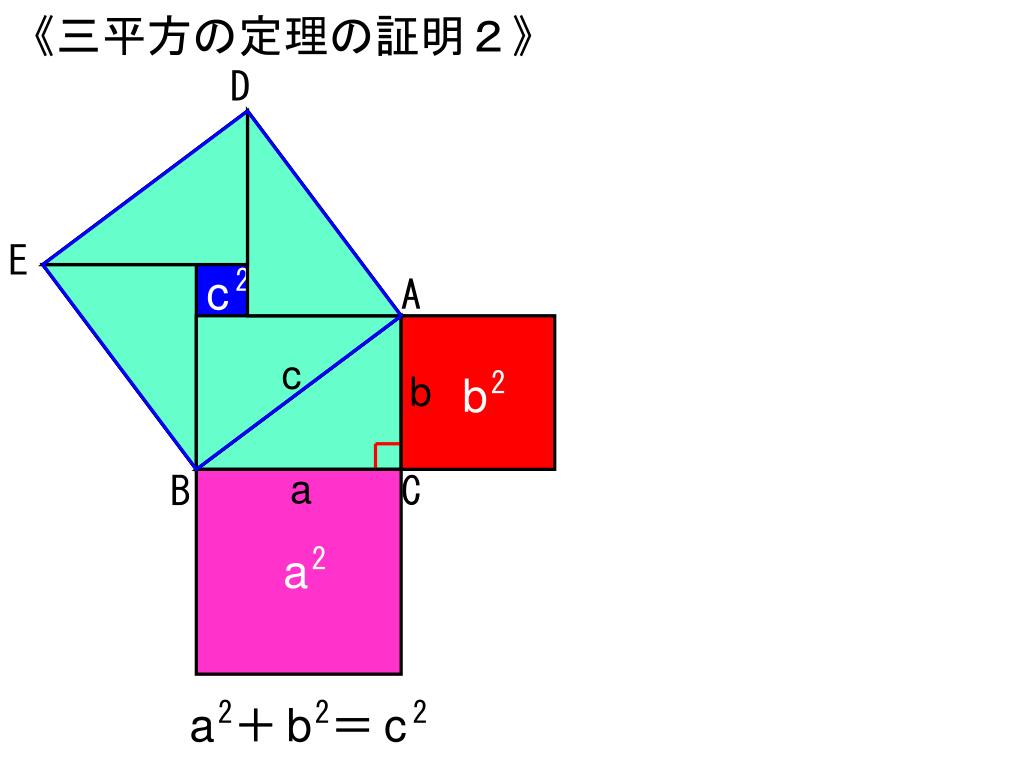 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 | 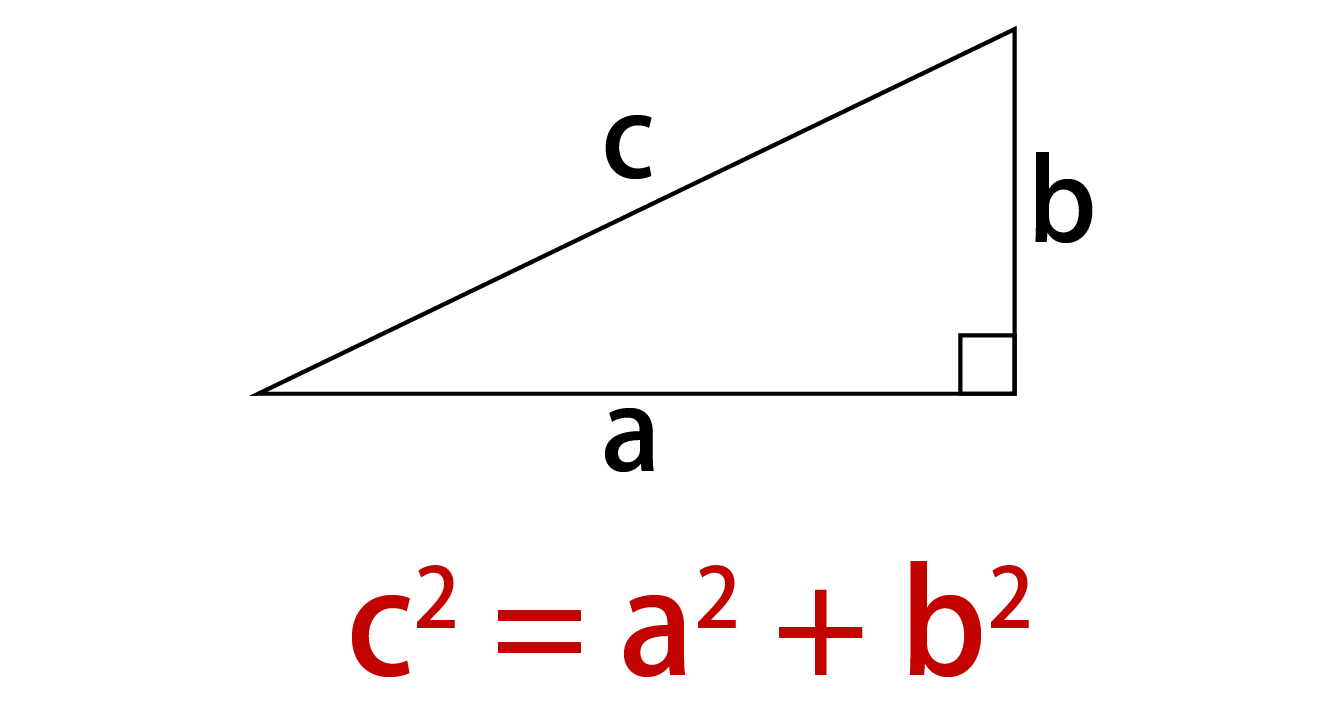 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 | 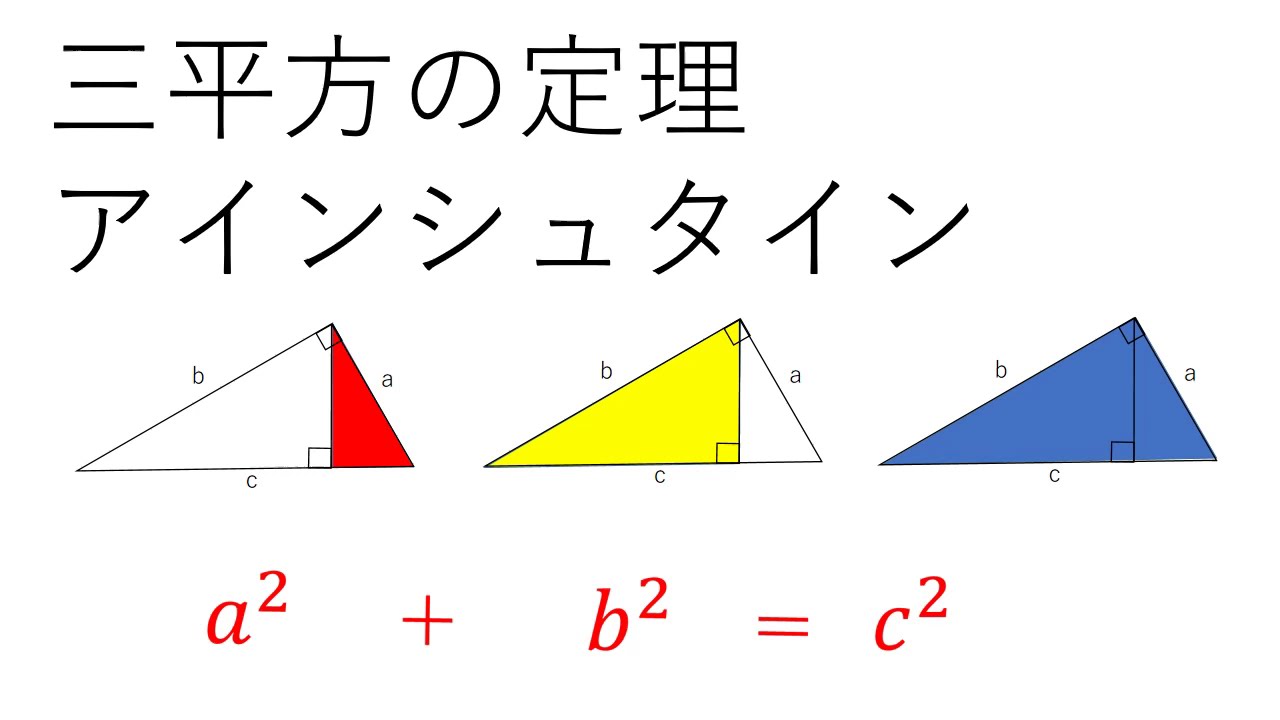三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |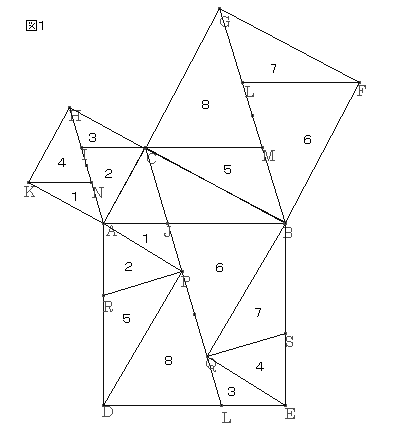
三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 | 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 | 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 | 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 | 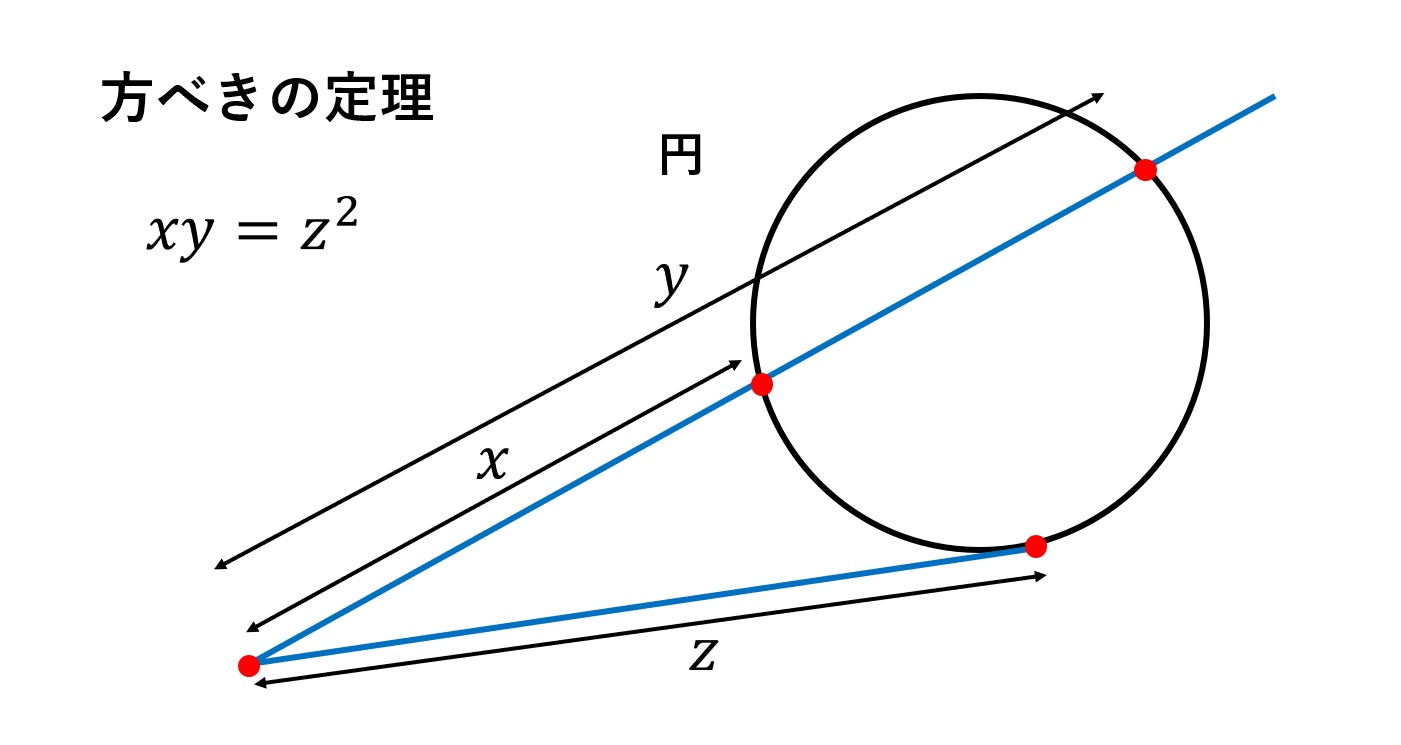 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 | 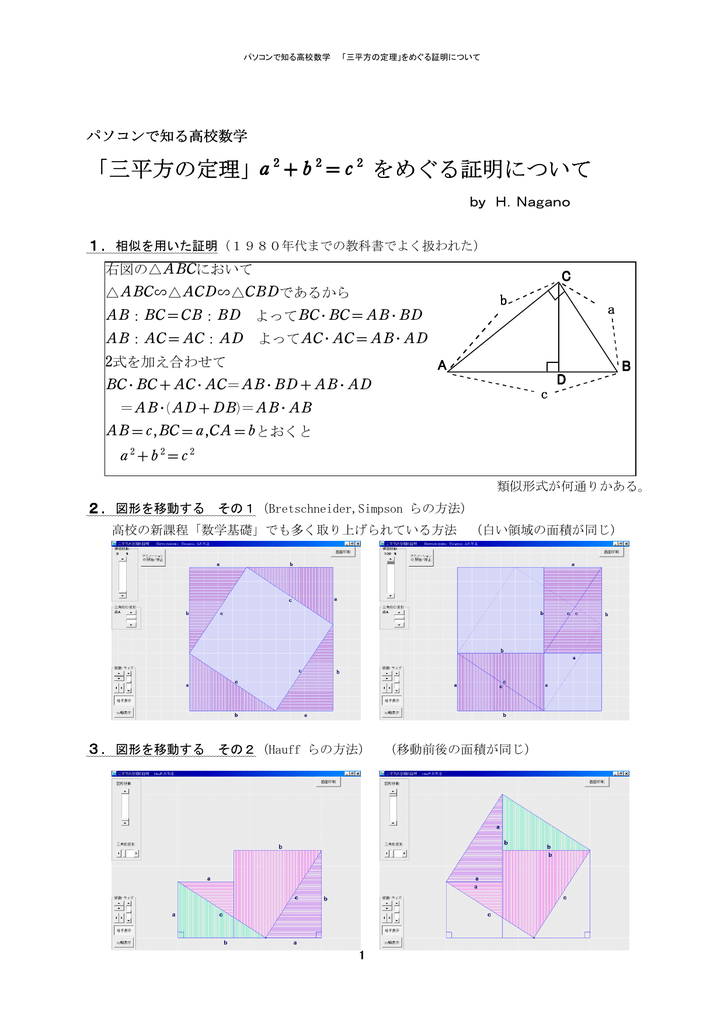 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 | 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 | 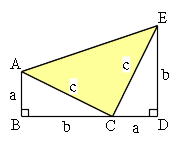 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 | 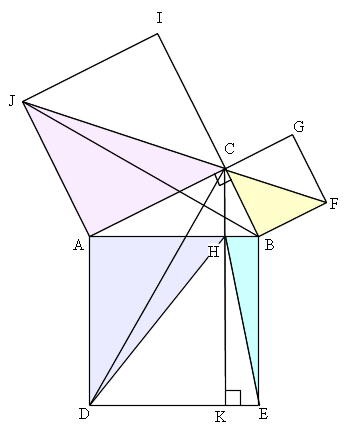 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
 三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |  三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学 |
2 二つの平方数の和で表す方法は何通りあるか 定理3 p が4k1 の形の素数である時、p は二つの平方数の和として（順序と符号を無視して）ちょうど1 通りに表される。 証明 素数p について表し方は高々1 通りであることを示せばよい。45°、45°、90°の直角三角形 (直角二等辺三角形)では 辺の比は必ず 11√2 三平方の定理の定理を使って計算すると簡単に証明することができます。
Incoming Term: 3平方の定理 証明, 3平方の定理 証明 いろいろ,
0 件のコメント:
コメントを投稿